Die Tiefensuche eines Diagramms beginnt an einem Scheitelpunkt im Diagramm und besucht vor dem Zurückverfolgen so weit wie möglich alle Scheitelpunkte im Diagramm.
Die Tiefensuche eines Diagramms ähnelt der Tiefensuche eines Baums, die in Tree Traversal, Tree Traversal, besprochen wird. Bei einem Baum beginnt die Suche an der Wurzel. In einem Diagramm kann die Suche an jedem Scheitelpunkt beginnen.

Eine Tiefensuche eines Baums besucht zuerst die Wurzel und dann rekursiv die Teilbäume der Wurzel. In ähnlicher Weise besucht die Tiefensuche eines Graphen zunächst einen Scheitelpunkt und dann rekursiv alle an diesen Scheitelpunkt angrenzenden Scheitelpunkte. Der Unterschied besteht darin, dass der Graph Zyklen enthalten kann, was zu einer unendlichen Rekursion führen könnte. Um dieses Problem zu vermeiden, müssen Sie die bereits besuchten Scheitelpunkte verfolgen.

Die Suche wird Tiefe-zuerst genannt, weil sie so weit wie möglich „tiefer“ im Diagramm sucht. Die Suche beginnt an einem Scheitelpunkt v. Nach dem Besuch von v wird ein nicht besuchter Nachbar von v besucht. Wenn v keinen nicht besuchten Nachbarn hat, kehrt die Suche zu dem Scheitelpunkt zurück, von dem aus sie v erreicht hat. Wir gehen davon aus, dass der Graph verbunden ist und die Suche beginnt Von jedem Scheitelpunkt aus können alle Scheitelpunkte erreicht werden.

Tiefensuchalgorithmus

Der Algorithmus für die Tiefensuche wird im folgenden Code beschrieben.

Eingabe: G = (V, E) und ein Startscheitelpunkt v
Ausgabe: ein DFS-Baum mit Wurzel v
1 Baum dfs(Vertex v) {
2 Besuch v;
3 für jeden Nachbarn w von v
4 if (w wurde nicht besucht) {
5 setze v als übergeordnetes Element für w im Baum;
6 dfs(w);
7 }
8 }

Sie können ein Array mit dem Namen isVisited verwenden, um anzugeben, ob ein Scheitelpunkt besucht wurde. Anfänglich ist isVisited[i] für jeden Scheitelpunkt i false. Sobald ein Scheitelpunkt, beispielsweise v, besucht wird, wird isVisited[v] auf true gesetzt.

Betrachten Sie die Grafik in Abbildung unten (a). Angenommen, wir starten die Tiefensuche am Scheitelpunkt 0. Besuchen Sie zuerst 0 und dann einen seiner Nachbarn, beispielsweise 1. Jetzt wird 1 besucht, wie in Abbildung unten (b) dargestellt. Scheitelpunkt 1 hat drei Nachbarn – 0, 2 und 4. Da 0 bereits besucht wurde, besuchen Sie entweder 2 oder 4. Wählen wir 2. Jetzt wird 2 besucht, wie in Abbildung unten (c) gezeigt. Scheitelpunkt 2 hat drei Nachbarn: 0, 1 und 3. Da 0 und 1 bereits besucht wurden, wählen Sie 3 aus. 3 ist jetzt besucht, wie in Abbildung unten (d) dargestellt. Zu diesem Zeitpunkt wurden die Scheitelpunkte in dieser Reihenfolge besucht:

0, 1, 2, 3

Da alle Nachbarn von 3 besucht wurden, gehen Sie zurück zu 2. Da alle Eckpunkte von 2 besucht wurden, gehen Sie zurück zu 1. 4 grenzt an 1, aber 4 wurde nicht besucht. Besuchen Sie daher 4, wie in der Abbildung unten (e) gezeigt. Da alle Nachbarn von 4 besucht wurden, kehren Sie zu 1 zurück.
Da alle Nachbarn von 1 besucht wurden, gehen Sie zurück zu 0. Da alle Nachbarn von 0 besucht wurden, endet die Suche.

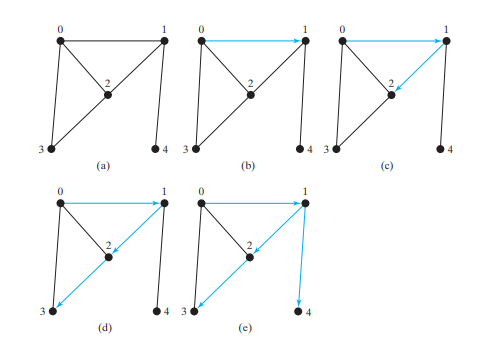
Da jede Kante und jeder Scheitelpunkt nur einmal besucht wird, beträgt die zeitliche Komplexität der Methode dfs O(|E| |V|), wobei |E | bezeichnet die Anzahl der Kanten und |V| die Anzahl der Eckpunkte.

Implementierung der Tiefensuche

Der Algorithmus für DFS im obigen Code verwendet Rekursion. Es ist natürlich, Rekursion zu verwenden, um es zu implementieren. Alternativ können Sie einen Stapel verwenden.

Die Methode dfs(int v) ist in den Zeilen 164–193 in AbstractGraph.java implementiert. Es gibt eine Instanz der Klasse Tree mit dem Scheitelpunkt v als Wurzel zurück. Die Methode speichert die gesuchten Scheitelpunkte in der Liste searchOrder (Zeile 165), das übergeordnete Element jedes Scheitelpunkts im Array parent (Zeile 166) und verwendet isVisited-Array, um anzuzeigen, ob ein Scheitelpunkt besucht wurde (Zeile 171). Es ruft die Hilfsmethode dfs(v, parent, searchOrder, isVisited) auf, um eine Tiefensuche durchzuführen (Zeile 174).

In der rekursiven Hilfsmethode beginnt die Suche am Scheitelpunkt u. u wird in Zeile 184 zu searchOrder hinzugefügt und als besucht markiert (Zeile 185). Für jeden nicht besuchten Nachbarn von u wird die Methode rekursiv aufgerufen, um eine Tiefensuche durchzuführen. Wenn ein Scheitelpunkt e.v besucht wird, wird das übergeordnete Element von e.v in parent[e.v] gespeichert (Zeile 189). Die Methode gibt zurück, wenn alle Scheitelpunkte für einen verbundenen Graphen oder in einer verbundenen Komponente besucht werden.

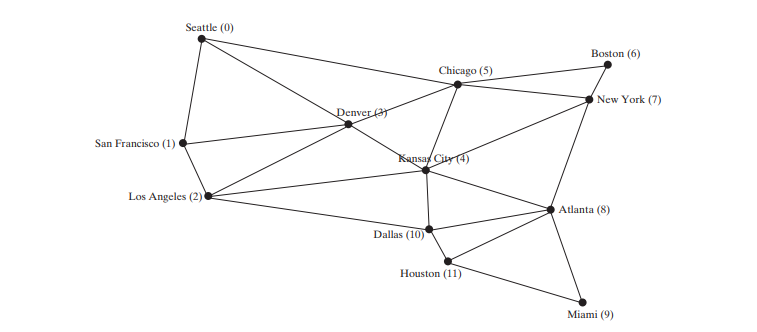
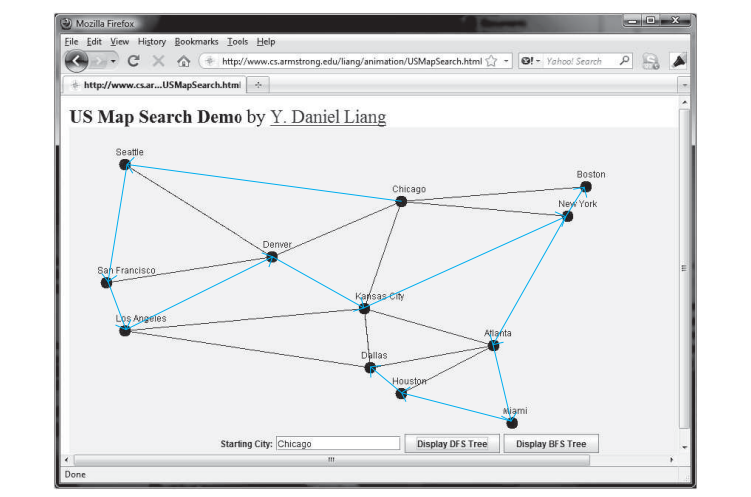
Der folgende Code gibt ein Testprogramm an, das ausgehend von Chicago ein DFS für das Diagramm in der Abbildung oben anzeigt. Die grafische Darstellung des DFS ab Chicago ist in der folgenden Abbildung dargestellt.

public class TestDFS {

    public static void main(String[] args) {
        String[] vertices = {"Seattle", "San Francisco", "Los Angeles", "Denver", "Kansas City", "Chicago", "Boston", "New York", "Atlanta", "Miami", "Dallas", "Houston"};

        int[][] edges = {
                {0, 1}, {0, 3}, {0, 5},
                {1, 0}, {1, 2}, {1, 3},
                {2, 1}, {2, 3}, {2, 4}, {2, 10},
                {3, 0}, {3, 1}, {3, 2}, {3, 4}, {3, 5},
                {4, 2}, {4, 3}, {4, 5}, {4, 7}, {4, 8}, {4, 10},
                {5, 0}, {5, 3}, {5, 4}, {5, 6}, {5, 7},
                {6, 5}, {6, 7},
                {7, 4}, {7, 5}, {7, 6}, {7, 8},
                {8, 4}, {8, 7}, {8, 9}, {8, 10}, {8, 11},
                {9, 8}, {9, 11},
                {10, 2}, {10, 4}, {10, 8}, {10, 11},
                {11, 8}, {11, 9}, {11, 10}
        };

        Graph graph = new UnweightedGraph(vertices, edges);
        AbstractGraph.Tree dfs = graph.dfs(graph.getIndex("Chicago"));

        java.util.List searchOrders = dfs.getSearchOrder();
        System.out.println(dfs.getNumberOfVerticesFound()   " vertices are searched in this DFS order:");
        for(int i = 0; i 



12 Scheitelpunkte werden in dieser DFS-Reihenfolge durchsucht:

 Chicago Seattle San Francisco Los Angeles Denver

 Kansas City New York Boston Atlanta Miami Houston Dallas

Muttergesellschaft von Seattle ist Chicago

Muttergesellschaft von San Francisco ist Seattle

Muttergesellschaft von Los Angeles ist San Francisco

Muttergesellschaft von Denver ist Los Angeles

Muttergesellschaft von Kansas City ist Denver

Muttergesellschaft von Boston ist New York

Muttergesellschaft von New York ist Kansas City

Muttergesellschaft von Atlanta ist New York

Muttergesellschaft von Miami ist Atlanta

Muttergesellschaft von Dallas ist Houston

Muttergesellschaft von Houston ist Miami




  
  
  Anwendungen der DFS


 Mit der Tiefensuche können viele Probleme gelöst werden, wie zum Beispiel die folgenden:

Erkennen, ob ein Diagramm verbunden ist. Durchsuchen Sie den Graphen ausgehend von einem beliebigen Scheitelpunkt. Wenn die Anzahl der gesuchten Eckpunkte mit der Anzahl der Eckpunkte im Diagramm übereinstimmt, ist das Diagramm verbunden. Andernfalls ist der Graph nicht verbunden.
Erkennen, ob es einen Pfad zwischen zwei Scheitelpunkten gibt.
Einen Pfad zwischen zwei Eckpunkten finden.
Alle verbundenen Komponenten finden. Eine verbundene Komponente ist ein maximal verbundener Teilgraph, in dem jedes Knotenpaar durch einen Pfad verbunden ist.
Erkennen, ob im Diagramm ein Zyklus vorhanden ist.
Einen Zyklus im Diagramm finden.
Suche nach einem Hamiltonschen Pfad/Zyklus. Ein Hamiltonscher Pfad in einem Diagramm ist ein Pfad, der jeden Scheitelpunkt im Diagramm genau einmal besucht. Ein Hamilton-Zyklus besucht jeden Scheitelpunkt im Diagramm genau einmal und kehrt zum Startscheitelpunkt zurück.
Die ersten sechs Probleme können einfach mit der dfs-Methode in AbstractGraph.java gelöst werden. Um einen Hamiltonschen Pfad/Zyklus zu finden, müssen Sie alle möglichen DFSs untersuchen, um denjenigen zu finden, der zum längsten Pfad führt. Der Hamilton-Pfad/Zyklus hat viele Anwendungen, unter anderem zur Lösung des bekannten Knight’s-Tour-Problems.