Einführung

In diesem Artikel demonstrieren wir einen vollständigen Projektworkflow für maschinelles Lernen mit Scikit-Learn. Wir werden ein Modell erstellen, um die Immobilienpreise in Kalifornien auf der Grundlage verschiedener Merkmale wie Durchschnittseinkommen, Hausalter und durchschnittliche Zimmeranzahl vorherzusagen. Dieses Projekt führt Sie durch jeden Schritt des Prozesses, einschließlich Laden der Daten, Erkundung, Modelltraining, Auswertung und Visualisierung der Ergebnisse. Egal, ob Sie ein Anfänger sind, der die Grundlagen verstehen möchte, oder ein erfahrener Praktiker, der eine Auffrischung sucht, dieser Artikel bietet wertvolle Einblicke in die praktische Anwendung maschineller Lerntechniken.

Projekt zur Vorhersage der Immobilienpreise in Kalifornien

1. Einführung

Der kalifornische Immobilienmarkt ist für seine einzigartigen Eigenschaften und Preisdynamik bekannt. In diesem Projekt wollen wir ein maschinelles Lernmodell entwickeln, um Immobilienpreise basierend auf verschiedenen Merkmalen vorherzusagen. Wir verwenden den kalifornischen Wohnungsdatensatz, der verschiedene Attribute wie Durchschnittseinkommen, Hausalter, durchschnittliche Zimmer und mehr enthält.

2. Bibliotheken importieren

In diesem Abschnitt importieren wir die notwendigen Bibliotheken für die Datenbearbeitung, Visualisierung und den Aufbau unseres maschinellen Lernmodells.

import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
from sklearn.datasets import fetch_california_housing

3. Laden des Datensatzes

Wir werden den California Housing-Datensatz laden und einen DataFrame erstellen, um die Daten zu organisieren. Die Zielvariable, der Hauspreis, wird als neue Spalte hinzugefügt.

# Load the California Housing dataset
california = fetch_california_housing()
df = pd.DataFrame(california.data, columns=california.feature_names)
df['PRICE'] = california.target

4. Zufällige Auswahl von Proben

Um die Analyse überschaubar zu halten, werden wir für unsere Studie zufällig 700 Proben aus dem Datensatz auswählen.

# Randomly Selecting 700 Samples
df_sample = df.sample(n=700, random_state=42)

5. Blick auf unsere Daten

Dieser Abschnitt bietet einen Überblick über den Datensatz und zeigt die ersten fünf Zeilen an, um die Merkmale und Struktur unserer Daten zu verstehen.

# Overview of the data
print("First five rows of the dataset:")
print(df_sample.head())

Ausgabe

First five rows of the dataset:
       MedInc  HouseAge  AveRooms  AveBedrms  Population  AveOccup  Latitude  \
20046  1.6812      25.0  4.192201   1.022284      1392.0  3.877437     36.06   
3024   2.5313      30.0  5.039384   1.193493      1565.0  2.679795     35.14   
15663  3.4801      52.0  3.977155   1.185877      1310.0  1.360332     37.80   
20484  5.7376      17.0  6.163636   1.020202      1705.0  3.444444     34.28   
9814   3.7250      34.0  5.492991   1.028037      1063.0  2.483645     36.62   

       Longitude    PRICE  
20046    -119.01  0.47700  
3024     -119.46  0.45800  
15663    -122.44  5.00001  
20484    -118.72  2.18600  
9814     -121.93  2.78000  

DataFrame-Informationen anzeigen

print(df_sample.info())

Ausgabe

Index: 700 entries, 20046 to 5350
Data columns (total 9 columns):
 #   Column      Non-Null Count  Dtype  
---  ------      --------------  -----  
 0   MedInc      700 non-null    float64
 1   HouseAge    700 non-null    float64
 2   AveRooms    700 non-null    float64
 3   AveBedrms   700 non-null    float64
 4   Population  700 non-null    float64
 5   AveOccup    700 non-null    float64
 6   Latitude    700 non-null    float64
 7   Longitude   700 non-null    float64
 8   PRICE       700 non-null    float64
dtypes: float64(9)
memory usage: 54.7 KB

Zusammenfassende Statistiken anzeigen

print(df_sample.describe())

Ausgabe

           MedInc    HouseAge    AveRooms   AveBedrms   Population  \
count  700.000000  700.000000  700.000000  700.000000   700.000000   
mean     3.937653   28.855714    5.404192    1.079266  1387.422857   
std      2.085831   12.353313    1.848898    0.236318  1027.873659   
min      0.852700    2.000000    2.096692    0.500000     8.000000   
25%      2.576350   18.000000    4.397751    1.005934   781.000000   
50%      3.480000   30.000000    5.145295    1.047086  1159.500000   
75%      4.794625   37.000000    6.098061    1.098656  1666.500000   
max     15.000100   52.000000   36.075472    5.273585  8652.000000   

         AveOccup    Latitude   Longitude       PRICE  
count  700.000000  700.000000  700.000000  700.000000  
mean     2.939913   35.498243 -119.439729    2.082073  
std      0.745525    2.123689    1.956998    1.157855  
min      1.312994   32.590000 -124.150000    0.458000  
25%      2.457560   33.930000 -121.497500    1.218500  
50%      2.834524   34.190000 -118.420000    1.799000  
75%      3.326869   37.592500 -118.007500    2.665500  
max      7.200000   41.790000 -114.590000    5.000010  

6. Aufteilen des Datensatzes in Trainings- und Testsätze

Wir werden den Datensatz in Features (X) und die Zielvariable (y) aufteilen und ihn dann in Trainings- und Testsätze für das Modelltraining und die Modellbewertung aufteilen.

# Splitting the dataset into Train and Test sets
X = df_sample.drop('PRICE', axis=1)  # Features
y = df_sample['PRICE']  # Target variable

# Split the dataset into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

7. Modellschulung

In diesem Abschnitt erstellen und trainieren wir ein lineares Regressionsmodell unter Verwendung der Trainingsdaten, um die Beziehung zwischen Merkmalen und Immobilienpreisen zu lernen.

# Creating and training the Linear Regression model
lr = LinearRegression()
lr.fit(X_train, y_train)

8. Bewertung des Modells

Wir werden Vorhersagen zum Testsatz treffen und den mittleren quadratischen Fehler (MSE) und die R-Quadrat-Werte berechnen, um die Leistung des Modells zu bewerten.

# Making predictions on the test set
y_pred = lr.predict(X_test)

# Calculating Mean Squared Error
mse = mean_squared_error(y_test, y_pred)
print(f"\nLinear Regression Mean Squared Error: {mse}")

Ausgabe

Linear Regression Mean Squared Error: 0.3699851092128846

9. Anzeige tatsächlicher und prognostizierter Werte

Hier erstellen wir einen DataFrame, um die tatsächlichen Hauspreise mit den von unserem Modell generierten prognostizierten Preisen zu vergleichen.

# Displaying Actual vs Predicted Values
results = pd.DataFrame({'Actual Prices': y_test.values, 'Predicted Prices': y_pred})
print("\nActual vs Predicted:")
print(results)

Ausgabe

Actual vs Predicted:
     Actual Prices  Predicted Prices
0          0.87500          0.887202
1          1.19400          2.445412
2          5.00001          6.249122
3          2.78700          2.743305
4          1.99300          2.794774
..             ...               ...
135        1.62100          2.246041
136        3.52500          2.626354
137        1.91700          1.899090
138        2.27900          2.731436
139        1.73400          2.017134

[140 rows x

 2 columns]

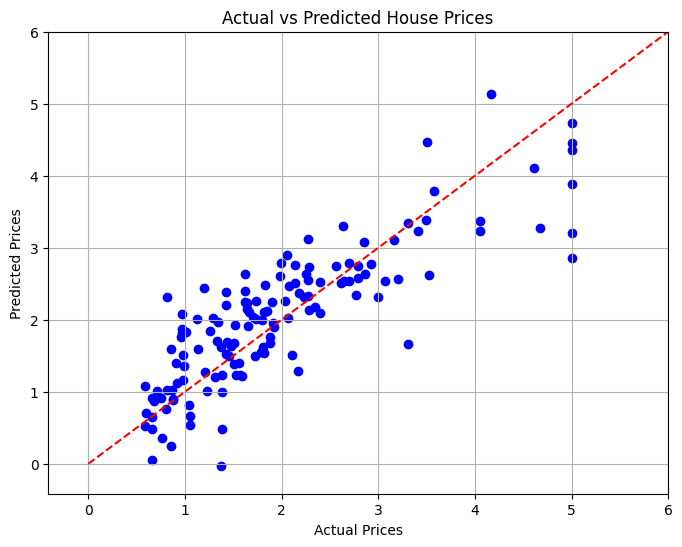
10. Visualisierung der Ergebnisse

Im letzten Abschnitt werden wir die Beziehung zwischen tatsächlichen und prognostizierten Immobilienpreisen mithilfe eines Streudiagramms visualisieren, um die Leistung des Modells visuell zu bewerten.

# Visualizing the Results
plt.figure(figsize=(8, 6))
plt.scatter(y_test, y_pred, color='blue')
plt.xlabel('Actual Prices')
plt.ylabel('Predicted Prices')
plt.title('Actual vs Predicted House Prices')

# Draw the ideal line
plt.plot([0, 6], [0, 6], color='red', linestyle='--')

# Set limits to minimize empty space
plt.xlim(y_test.min() - 1, y_test.max()   1)
plt.ylim(y_test.min() - 1, y_test.max()   1)

plt.grid()
plt.show()

Abschluss

In diesem Projekt haben wir ein lineares Regressionsmodell entwickelt, um die Immobilienpreise in Kalifornien anhand verschiedener Merkmale vorherzusagen. Der mittlere quadratische Fehler wurde berechnet, um die Leistung des Modells zu bewerten, was ein quantitatives Maß für die Vorhersagegenauigkeit lieferte. Durch die Visualisierung konnten wir sehen, wie gut unser Modell im Vergleich zu tatsächlichen Werten abschneidet.

Dieses Projekt demonstriert die Leistungsfähigkeit des maschinellen Lernens in der Immobilienanalyse und kann als Grundlage für fortgeschrittenere Vorhersagemodellierungstechniken dienen.