1. Avoiding Confusing File Names in VS Code

When writing C files in VS Code, I named a file first.c.cpp. After completing the program, I encountered errors during execution. After 30 minutes of troubleshooting, I discovered the issue lay in the file name:
The .c extension led the IDE to mistakenly identify it as a C program, causing VS Code to use gcc (the C compiler) instead of g (the C compiler) to compile my code.

Caption: How fool!

• Solution: In the tasks.json file, change the 'command' line from gcc to g .
• Lesson learned: Use clear .cpp extensions for C files to avoid unnecessary confusion.

2. Java's Cross-Platform Design Philosophy

Java's design philosophy differs significantly from traditional compiled languages:

Traditional Compilation:

1. Languages like C compile directly into machine code for specific platforms (e.g., Windows, Mac, Linux)
2. The resulting executable files (.exe) can only run on the target platform

Java's Approach:

1. The compiler generates intermediate code (bytecode)
2. This bytecode can run on any platform with a Java Virtual Machine (JVM) installed
3. The JVM is responsible for translating the bytecode into machine code for the current platform

This design achieves the goal of "Write Once, Run Anywhere," whereas C executables (.exe files) are limited to running on a single platform.

• Advantages:The same program can run on different computers without modification

• Disadvantages:The additional step in the process can make compilation slightly slower compared to traditional methods

Write once, Run anywhere

                             ---------James Gosling

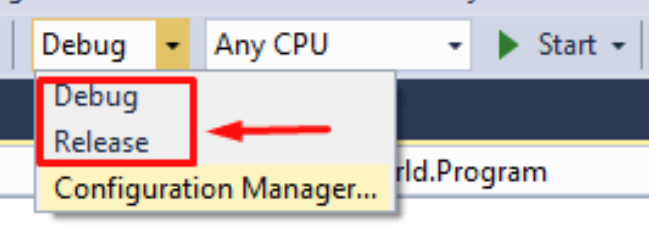
3. Two Common Compilation Modes

• Debug mode is oriented towards debugging, with fewer optimizations. It's mainly used for debugging programs.
• Release mode is primarily used for generating the release version, focusing on optimization and only retaining basic debugging functionality.

4. Understanding Forced Type Casting from a Low-Level Perspective

Little Endian: The least significant byte is stored at the lowest address. This storage method emerged to facilitate CPU memory reading, which occurs from low to high addresses. Interestingly, this is opposite to humans typically write numbers.
For example:
Binary representation of 329933 is 00000000 00000101 00001000 11001101
Little Endian storage: 11001101 00001000 00000101 00000000
As we can see, Little Endian reverses the order of bytes in the binary representation. However, it's crucial to note that the bit order within each byte remains unchanged!

A Fun Game to Understand Forced Type Casting

My favorite experiment for introducing type casting!

# include 
int main()

{
    int a;

    int *p;

    a=329933;

    p=&a;

    char *q;

    q=(char*)p;

    printf("%d\n",*p);

    printf("%d\n",*q);

}

Output:

329933
-51

I'm curious why it outputs -51?

Explanation

1. (char*)&a points to the first byte of the int. The first byte 11001101is interpreted as a char.
2. The highest bit 1 indicates a negative number, after two's complement conversion, we get -51 (those friends who are familiar with two's complement can verify if it indeed represents -51)

Is this a coincidence? Let's try two more examples

printf("%d\n",*(q 1));
printf("%d\n",*(q 2));

Try it:

1. Try running the code mentioned above and observe the output.
2. Consider why the second and third bytes produce such output. Feel free to discuss this in the comments section.
3. Can you apply forced type casting to other data types? Give it a try!

Additional Info: Two's Complement

When performing forced type casting, (char)p will point to the address of the first byte of the four-byte int, which is 11001101.
The leftmost 1 represents the negative sign, indicating it's a negative number. After applying two's complement, we get: 0110011 (the last 7 bits)

(Note: For positive numbers, the two's complement is simply the binary representation of the decimal number. For negative numbers, the two's complement is obtained by inverting all bits except the leftmost (highest) bit, then adding 1 to the rightmost bit.)

Converting this to decimal gives us -51. Interesting, right?

Benefits of Two's Complement:

1. It allows both positive and integer types to be calculated using only an adder, eliminating the need for a subtractor and simplifying hardware need.
2. It provides a unique binary representation for zero. 10000000 doesn't represent -0, but -128, while 00000000 represents 0, not 0.

Many people wonder why it's -128. If you know the answer, feel free to share it in the comments section. This will not only help others but also help you organize your thoughts.