Imagine if you could only use straight lines, ellipses, and circles, wouldn't it be difficult to design a car with smooth lines and a complex appearance?

In 1962, the French engineer Pierre Bézier published the Bézier curve, which was initially used for the main body design of cars.

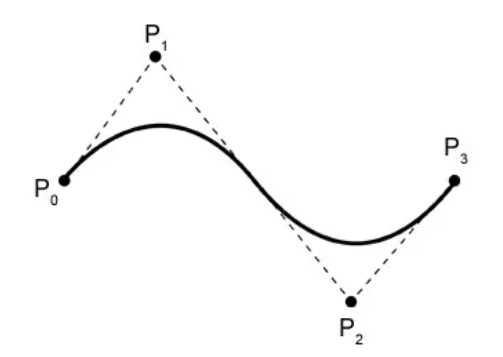
Bézier curves can define a smooth curve through a series of control points. The curve always passes through the first and last control points and is influenced by the shape of the intermediate control points. Additionally, Bézier curves have the property of convex hulls.

Bézier curves are widely used in computer graphics and image modeling, such as in animation, font design, and industrial design.

Formula

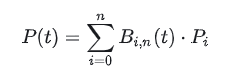
Let's understand this.

P(t) represents a point on the curve at t (t is a fraction, with a value from 0 to 1). What is a point on the curve at t? A common curve description is: y = f(x), and for now, let's understand P(t) as f(x). The difference is that P(t) is a parametric representation (and the calculation result is a "vector" like [x, y]), which will be explained in detail later.

Next, Pi represents the i-th control point (i starts from 0). Taking the above figure as an example, there are 4 control points, which are P0, P1, P2, P3. The n in the formula is the last index of the control points, that is, n = 3 (note that it is not the number of control points, but the count minus 1).

Bi,n(t) is the Bernstein basis function, also known as the basis function. For each specific (i, n), there is a different basis function corresponding to it. If you understand from a weighted perspective, you can consider the basis function as a weight function, indicating the "contribution" of the i-th control point Pi to the curve coordinates at the position of t.

The formula for the basis function is as follows:

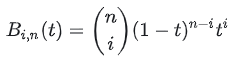
$\left(\genfrac{}{}{0px}{}{n}{i}\right)$(in​) Is the combination number (how many ways to choose i out of n?). As for why the basis function looks like this, it can be understood in connection with the De Casteljau algorithm (see later in the text)

Back to the P(t) formula, ${\sum }_{i=0}^n$∑i=0n​ is the summation symbol, indicating that the subsequent part ( $B_{i,n}(t)\cdot P_i$Bi,n​(t)⋅Pi​ ) is to be summed from i=0 to i=n.

Taking the above figure as an example, assuming we want to calculate P(0.1), how to do it? It is expanded as follows:

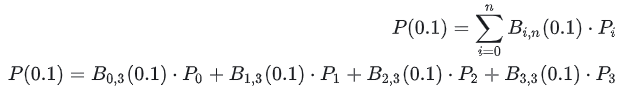
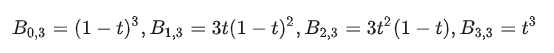
Substitute t=0.1 to get:

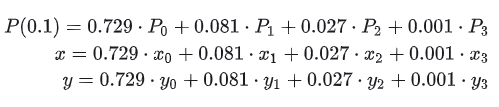
Parametric representation of the curve

Here directly cites an article from a netizen (link)

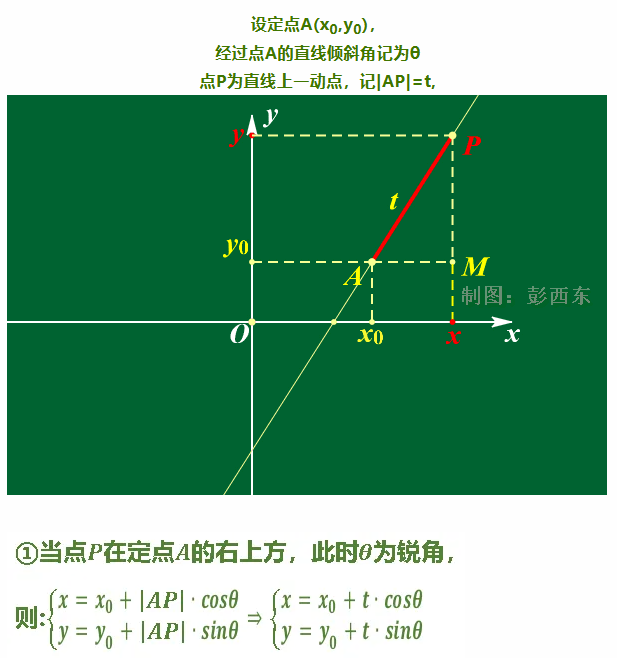
Let's focus on the formula above.

As shown in the figure above, the straight line we are familiar with can be understood from another perspective: using t (i.e., the length of |AP| from the point P to the known point (x0,y0)), then point P can be determined through the above trigonometric functions.

More generally, it can be written as:

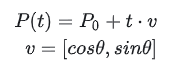
Here, P0 is the vector [x0,y0]and v is also a vector. When added together, P(t)is the vector [x,y].

Looking at the circle again:

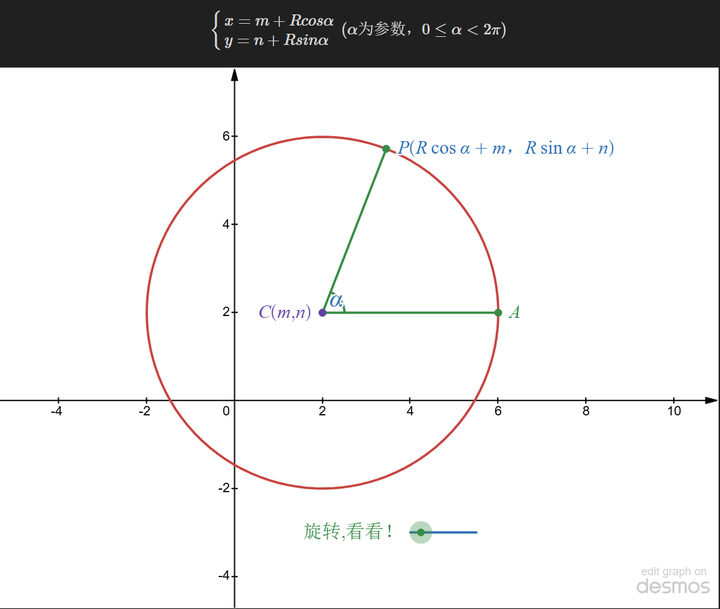
As shown in the diagram, the circle can be viewed as having a known center, with any point on the circle being determined by the rotation angle and the radius. It can also be written as:

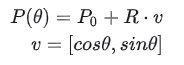
The parametric equations maintain geometric invariance and can represent shapes like circles (where one x corresponds to multiple y values).

De Casteljau

The De Casteljau algorithm is a method used in practical applications to evaluate and approximate Bézier curves for drawing and other operations. Compared to the previous definition-based evaluation method, it is faster and more stable, and closer to the characteristics of Bézier curves.

Here, we refer to two articles: link1 and link2

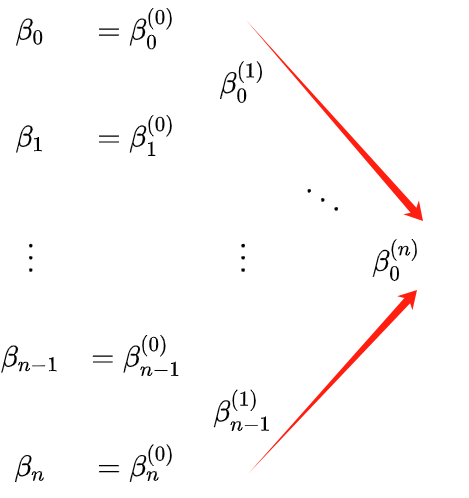
Firstly, the following is defined:

Look at the above β. It's a bit confusing with the superscripts and subscripts; you can use the following triangular recursion for understanding:

The red edges of the triangle in the above figure are the control points of the two segments divided by t0. To more vividly understand t0, P(t0) （i.e., ${\beta }_0^{(n)}$β0(n)​ ）, the control points of the two curves, you can refer to the following figure:

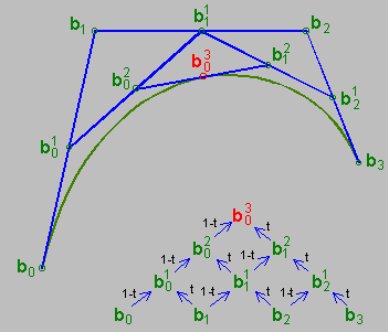
The figure above demonstrates the relationships between various points when t=0.5.

From the perspective of "interpolation," the calculation process can also be understood as:

1. Finding the midpoints of each pair of adjacent control points (because t=0.5), that is, b01, b11, b21 (please forgive my notation; writing in LaTeX is too troublesome)
2. Find the midpoint b02 on b01−b11, and find the midpoint b12 on b11-b21
3. Find the midpoint b03 on b02−b12 ​ In fact, the essence of the De Casteljau algorithm is interpolation and iteration.

Curve Drawing Based on De Casteljau

Currently, two methods are observed.

One method involves traversing t from 0 to 1 with small step increments（i.e. 0.01). Each time P(t) is sought, a recursive formula is used to determine ${\beta }_0^{(n)}$β0(n)​ .

The other method involves seeking P(t=0.5), and then for the two divided curves, P(t=0.5) is sought respectively... This subdivision continues until the curve is approximated.

Implementation

It always feels unreal to just watch without practicing.

So I wrote my own implementation code for curve drawing and organized it into a toolkit: Compilelife's Toolkit

Corresponding core code is here