Introduction 1

The process in which a function calls itself is called recursion and the
corresponding function is called a recursive function.
Since computer programming is a fundamental application of mathematics, so let
us first try to understand the mathematical reasoning behind recursion.
In general, we all are aware of the concept of functions. In a nutshell, functions are
mathematical equations that produce an output when providing input. For example:
Suppose the function F(x) is a function defined by: F(x) = x^2 4
We can write the Java Code for this function as:

public static int F(int x){
return (x * x 4);
}

Now, we can pass different values of x to this function and receive our output
accordingly.
Before moving on to the recursion, let's try to understand another mathematical
concept known as the Principle of Mathematical Induction (PMI).

Principle of Mathematical Induction (PMI) is a technique for proving a statement, a
formula, or a theorem that is asserted about a set of natural numbers. It has the
following three steps:
1.** Step of the trivial case*: In this step, we will prove the desired statement for
a base case like n = 0 or n = 1.
2.* Step of assumption**: In this step, we will assume that the desired statement
is valid for n = k.

1. To prove step: From the results of the assumption step, we will prove that, n = k 1 is also true for the desired equation whenever n = k is true.

For Example: Let’s prove using the Principle of Mathematical Induction that:
S(N): 1 2 3 ... N = (N * (N 1))/2
(The sum of first N natural numbers)
Proof:
Step 1: For N = 1, S(1) = 1 is true.
Step 2: Assume, the given statement is true for N = k, i.e.,
1 2 3 .... k = (k * (k 1))/2
Step 3: Let’s prove the statement for N = k 1 using step 2.

To Prove: 1 2 3 ... (k 1) = ((k 1)*(k 2))/2
Proof:

Adding (k 1) to both LHS and RHS in the result obtained on step 2:
1 2 3 ... (k 1) = (k*(k 1))/2 (k 1)

Now, taking (k 1) common from RHS side:
1 2 3 ... (k 1) = (k 1)*((k 2)/2)

According to the statement that we are trying to prove:
1 2 3 ... (k 1) = ((k 1)*(k 2))/2
Hence proved.

Working of recursion

We can define the steps of the recursive approach by summarizing the above three
steps:
● Base case: A recursive function must have a terminating condition at which
the process will stop calling itself. Such a case is known as the base case. Without a base case, it will keep calling itself and get stuck in an
infinite loop. Soon, the recursion depth* will be exceeded and it will throw
an error.
● Recursive call: The recursive function will invoke itself on a smaller version
of the main problem. We need to be careful while writing this step as it is
crucial to correctly figure out what your smaller problem is.
● Small calculation: Generally, we perform a calculation step in each recursive
call. We can achieve this calculation step before or after the recursive call
depending upon the nature of the problem.

Note: Recursion uses an in-built stack that stores recursive calls. Hence, the
number of recursive calls must be as small as possible to avoid memory overflow. If
the number of recursion calls exceeds the maximum permissible amount, the
**recursion depth** will be exceeded.
Now, let us see how to solve a few common problems using Recursion

Problem Statement - Find Factorial of a Number

Approach: Figuring out the three steps of PMI and then relating the same using
recursion

1. Induction Step: Calculating the factorial of a number n - F(n) Induction Hypothesis: We have already obtained the factorial of n-1 - F(n-1)
2. Expressing F(n) in terms of F(n-1): F(n)=n*F(n-1). Thus we get

public static int fact(int n){
int ans = fact(n-1); #Assumption step
return ans * n; #Solving problem from assumption step
}

1. The code is still not complete. The missing part is the base case. Now we will dry run to find the case where the recursion needs to stop. Consider n = 5:

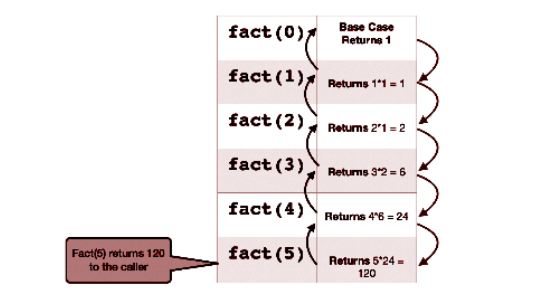
As we can see above, we already know the answer of n = 0, which is 1. So we will
keep this as our base case. Hence, the code now becomes:

public static int factorial(int n){
if (n == 0) // base case
return 1;
else
return n*factorial(n-1); // recursive case
}