Entropix: Sampling Techniques for Maximizing Inference Performance

According to the Entropix README, Entropix uses an entropy-based sampling method. This article explains the specific sampling techniques based on entropy and varentropy.

Entropy and Varentropy

Let's start by explaining entropy and varentropy, as these are key factors in determining the sampling strategy.

Entropy

In information theory, entropy is a measure of the uncertainty of a random variable. The entropy of a random variable X is defined by the following equation:

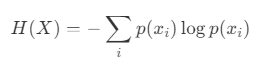
• X: A discrete random variable.
• x_i: The i-th possible state of X.
• p(x_i): The probability of state x_i.

Entropy is maximized when the probability distribution is uniform. Conversely, when a specific state is much more likely than others, entropy decreases.

Varentropy

Varentropy, closely related to entropy, represents the variability in the information content. Considering the information content I(X), entropy H(X), and variance for a random variable X, varentropy V E(X) is defined as follows:

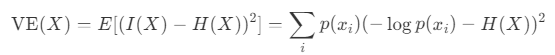
Varentropy becomes large when the probabilities p(x_i) vary greatly. It becomes small when the probabilities are uniform—either when the distribution has maximum entropy or when one value has a probability of 1 and all others have a probability of 0.

Sampling Methods

Next, let's explore how sampling strategies change based on entropy and varentropy values.

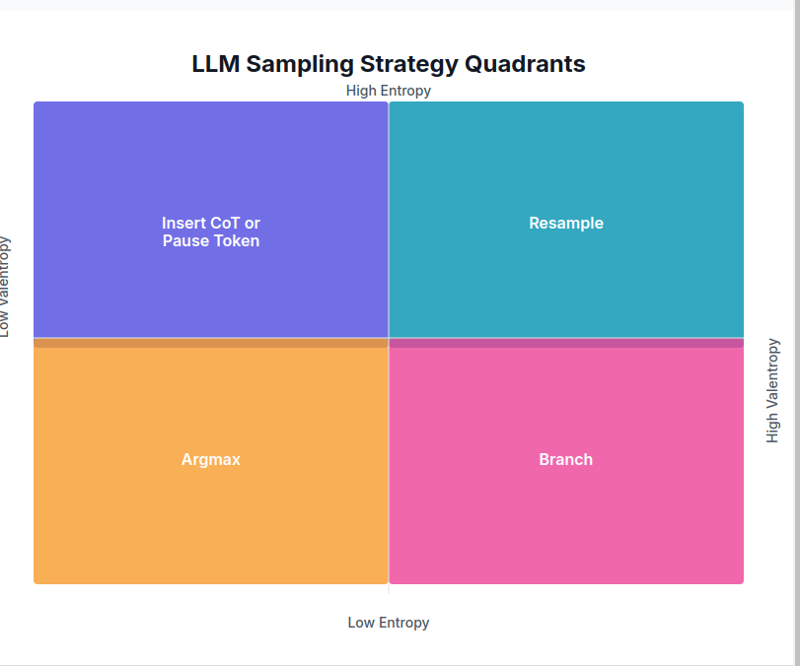
1. Low Entropy, Low Varentropy → Argmax

In this scenario, a particular token has a much higher prediction probability than the others. Since the next token is almost certain, Argmax is used.

if ent 



Code link


  
  
  2. Low Entropy, High Varentropy → Branch


This occurs when there is some confidence, but multiple viable options exist. In this case, the Branch strategy is used to sample from multiple choices and select the best outcome.


elif ent  5.0:
    temp_adj = 1.2   0.3 * interaction_strength
    top_k_adj = max(5, int(top_k * (1   0.5 * (1 - agreement))))
    return _sample(logits, temperature=min(1.5, temperature * temp_adj), top_p=top_p, top_k=top_k_adj, min_p=min_p, generator=generator)




Code link

Although this strategy is called "Branch," the current code appears to adjust the sampling range and select a single path. (If anyone has more insight, further clarification would be appreciated.)


  
  
  3. High Entropy, Low Varentropy → CoT or Insert Pause Token


When the prediction probabilities of the next token are fairly uniform, indicating that the next context is not certain, a clarification token is inserted to resolve the ambiguity.


elif ent > 3.0 and vent 



Code link


  
  
  4. High Entropy, High Varentropy → Resample


In this case, there are multiple contexts, and the prediction probabilities of the next token are low. A resampling strategy is used with a higher temperature setting and a lower top-p.


elif ent > 5.0 and vent > 5.0:
    temp_adj = 2.0   0.5 * attn_vent
    top_p_adj = max(0.5, top_p - 0.2 * attn_ent)
    return _sample(logits, temperature=max(2.0, temperature * temp_adj), top_p=top_p_adj, top_k=top_k, min_p=min_p, generator=generator)




Code link


  
  
  Intermediate Cases


If none of the above conditions are met, adaptive sampling is performed. Multiple samples are taken, and the best sampling score is calculated based on entropy, varentropy, and attention information.


else:
    return adaptive_sample(
        logits,
        metrics,
        gen_tokens,
        n_samples=5,
        base_temp=temperature,
        base_top_p=top_p,
        base_top_k=top_k,
        generator=generator
    )




Code link



  
  
  References

• Entropix Repository
• What is Entropix Doing?