1. تجنب الخلط بين أسماء الملفات في VS Code

عند كتابة ملفات C في VS Code، قمت بتسمية الملف first.c.cpp. بعد الانتهاء من البرنامج، واجهت أخطاء أثناء التنفيذ. بعد 30 دقيقة من استكشاف الأخطاء وإصلاحها، اكتشفت أن المشكلة تكمن في اسم الملف:
أدى الامتداد .c إلى قيام IDE بتعريفه عن طريق الخطأ على أنه برنامج C، مما تسبب في استخدام VS Code لـ gcc (مترجم C) بدلاً من g (مترجم C) لتجميع الكود الخاص بي.

التسمية التوضيحية: يا له من أحمق!

• الحل: في ملف Tasks.json، قم بتغيير سطر "الأمر" من gcc إلى g .
• الدرس المستفاد: استخدم امتدادات .cpp الواضحة لملفات C لتجنب الالتباس غير الضروري.

2. فلسفة التصميم عبر الأنظمة الأساسية لجافا

تختلف فلسفة تصميم جافا بشكل كبير عن اللغات التقليدية المترجمة:

التجميع التقليدي:

1. يتم تجميع لغات مثل C مباشرة في كود الجهاز لأغراض محددة الأنظمة الأساسية (مثل Windows وMac وLinux)
2. لا يمكن تشغيل الملفات القابلة للتنفيذ الناتجة (.exe) إلا على النظام الأساسي المستهدف

نهج جافا:

1. يقوم المترجم بإنشاء كود وسيط (رمز بايت)
2. يمكن تشغيل هذا الرمز الثانوي على أي نظام أساسي مثبت عليه Java Virtual Machine (JVM)
3. JVM مسؤول عن ترجمة الرمز الثانوي إلى رمز الجهاز للنظام الأساسي الحالي

يحقق هذا التصميم هدف "الكتابة مرة واحدة، والتشغيل في أي مكان،" بينما تقتصر ملفات C التنفيذية (ملفات .exe) على التشغيل على نظام أساسي واحد.

• المميزات: يمكن تشغيل نفس البرنامج على أجهزة كمبيوتر مختلفة دون تعديل

• العيوب : الخطوة الإضافية في العملية يمكن أن تجعل التجميع أبطأ قليلاً مقارنة بالطرق التقليدية

اكتب مرة واحدة، قم بالتشغيل في أي مكان

                             ---------James Gosling

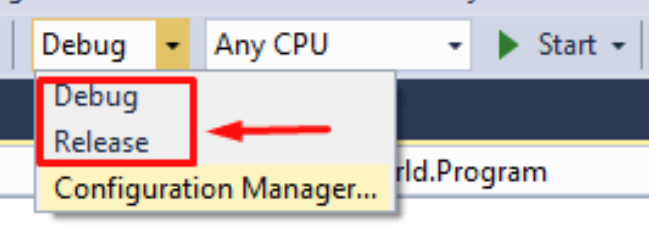
3. وضعان مشتركان للتجميع

• يتم توجيه وضع التصحيح نحو تصحيح الأخطاء، مع تحسينات أقل. يتم استخدامه بشكل أساسي لبرامج التصحيح.
• يتم استخدام وضع الإصدار بشكل أساسي لإنشاء إصدار الإصدار، مع التركيز على التحسين والاحتفاظ فقط بوظيفة تصحيح الأخطاء الأساسية.

4. فهم صب النوع القسري من منظور منخفض المستوى

Little Endian: يتم تخزين البايت الأقل أهمية في العنوان الأدنى. ظهرت طريقة التخزين هذه لتسهيل قراءة ذاكرة وحدة المعالجة المركزية، والتي تحدث من العناوين المنخفضة إلى العناوين العالية. ومن المثير للاهتمام أن هذا عكس ما يكتبه البشر عادة من أرقام.
على سبيل المثال:
التمثيل الثنائي لـ 329933 هو 00000000 00000101 00001000 11001101
تخزين إنديان الصغير: 11001101 00001000 00000101 00000000
كما نرى، يقوم Little Endian بعكس ترتيب البايتات في التمثيل الثنائي. ومع ذلك، من المهم ملاحظة أن ترتيب البت داخل كل بايت يظل دون تغيير!

لعبة ممتعة لفهم اختيار النوع القسري

تجربتي المفضلة في تقديم نوع الكتابة!

# include 
int main()

{
    int a;

    int *p;

    a=329933;

    p=&a;

    char *q;

    q=(char*)p;

    printf("%d\n",*p);

    printf("%d\n",*q);

}

الإخراج:

329933
-51

أتساءل لماذا ينتج -51؟

توضيح

1. (char*)&a يشير إلى البايت الأول من int. يتم تفسير البايت الأول 11001101 على أنه حرف.
2. يشير أعلى بت 1 إلى رقم سالب، وبعد تحويل تكملة اثنين، نحصل على -51 (يمكن لهؤلاء الأصدقاء الذين هم على دراية بتكملة اثنين التحقق مما إذا كان يمثل بالفعل -51)

هل هذه صدفة؟ لنجرب مثالين آخرين

printf("%d\n",*(q 1));
printf("%d\n",*(q 2));

جربه:

1. حاول تشغيل الكود المذكور أعلاه ولاحظ النتيجة.
2. فكر في سبب إنتاج البايتتين الثانية والثالثة لمثل هذا الإخراج. لا تتردد في مناقشة هذا الأمر في قسم التعليقات.
3. هل يمكنك تطبيق صب النوع القسري على أنواع البيانات الأخرى؟ جربها!

معلومات إضافية: تكملة لشخصين

عند إجراء عملية تحويل النوع القسري، سيشير (char)p إلى عنوان البايت الأول من int ذو الأربعة بايت، وهو 11001101.
يمثل الرقم 1 في أقصى اليسار الإشارة السالبة، مما يشير إلى أنه رقم سالب. وبعد تطبيق تكملة الاثنين نحصل على: 0110011 (آخر 7 بتات)

(ملاحظة: بالنسبة للأرقام الموجبة، فإن تكملة الاثنين هي ببساطة التمثيل الثنائي للرقم العشري. بالنسبة للأرقام السالبة، يتم الحصول على تكملة الاثنين عن طريق قلب جميع البتات باستثناء البت الموجود في أقصى اليسار (الأعلى)، ثم إضافة 1 إلى أقصى اليمين.)

تحويل هذا إلى عدد عشري يعطينا -51. مثير للاهتمام، أليس كذلك؟

فوائد تكملة اثنين:

1. يسمح بحساب كلا النوعين الموجب والأعداد الصحيحة باستخدام أداة الجمع فقط، مما يلغي الحاجة إلى أداة الطرح وتبسيط الحاجة إلى الأجهزة.
2. يوفر تمثيلاً ثنائيًا فريدًا للصفر. 10000000 لا يمثل -0، بل -128، بينما 00000000 يمثل 0، وليس 0.

يتساءل الكثير من الناس عن سبب وجود -128. إذا كنت تعرف الإجابة، فلا تتردد في مشاركتها في قسم التعليقات. لن يساعد هذا الآخرين فحسب، بل سيساعدك أيضًا على تنظيم أفكارك.