يمكن اختزال مسألة التسعة ذيول الموزونة إلى مشكلة أقصر مسار مرجح.
قدم القسم مشكلة التسعة ذيول وحلها باستخدام خوارزمية BFS. يعرض هذا القسم شكلًا مختلفًا من المشكلة ويحلها باستخدام خوارزمية المسار الأقصر.

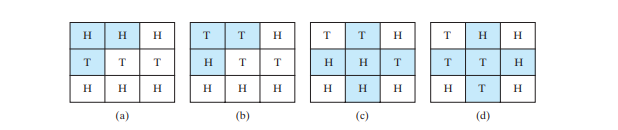
تتمثل مشكلة التسعة ذيول في العثور على الحد الأدنى لعدد الحركات التي تؤدي إلى توجيه جميع العملات المعدنية لأسفل. كل حركة تقلب العملة الرئيسية وجيرانها. تقوم مسألة التسعة ذيول الموزونة بتعيين عدد التقلبات كوزن في كل حركة. على سبيل المثال، يمكنك تغيير العملات المعدنية في الشكل أدناه أ إلى تلك الموجودة في الشكل أدناه ب عن طريق قلب العملة الأولى في الصف الأول وجارتيها. وبالتالي، فإن وزن هذه الخطوة هو 3. يمكنك تغيير العملات المعدنية في الشكل أدناه c إلى الشكل أدناه d عن طريق قلب العملة المركزية وجيرانها الأربعة. لذا فإن وزن هذه الحركة هو 5.

يمكن تقليل مشكلة التسعة ذيول الموزونة إلى إيجاد أقصر مسار من عقدة البداية إلى العقدة المستهدفة في رسم بياني مرجح الحافة. يحتوي الرسم البياني على 512 عقدة. أنشئ حافة من العقدة v إلى u إذا كان هناك انتقال من العقدة u إلى العقدة v. قم بتعيين عدد التقلبات ليكون وزن الحافة.

تذكر أننا في القسم قمنا بتعريف فئة NineTailModel لنمذجة مشكلة التسعة ذيول. نحدد الآن فئة جديدة تسمى WeightedNineTailModel التي تمتد إلى NineTailModel، كما هو موضح في الشكل أدناه.

تنشئ فئة NineTailModel رسمًا بيانيًا وتحصل على شجرة متجذرة في العقدة المستهدفة 511. WeightedNineTailModel هو نفس NineTailModel باستثناء أنه يقوم بإنشاء WeightedGraph ويحصل على ShortestPathTree المتجذر في العقدة المستهدفة 511. WeightedNineTailModel يمتد NineTailModel. تبحث الطريقة getEdges() عن جميع الحواف في الرسم البياني. تقوم طريقة getNumberOfFlips(int u, int v) بإرجاع عدد مرات التقليب من العقدة u إلى العقدة v. تقوم الطريقة getNumberOfFlips(int u) بإرجاع عدد مرات التقليب من العقدة u إلى العقدة المستهدفة.

WeightedNineTailModel.

package demo;
import java.util.*;

public class WeightedNineTailModel extends NineTailModel {
    /** Construct a model */
    public WeightedNineTailModel() {
        // Create edges
        List edges = getEdges();

        // Create a graph
        WeightedGraph graph = new WeightedGraph(edges, NUMBER_OF_NODES);

        // Obtain a shortest path tree rooted at the target node
        tree = graph.getShortestPath(511);
    }

    /** Create all edges for the graph */
    private List getEdges() {
        // Store edges
        List edges = new ArrayList();

        for(int u = 0; u .ShortestPathTree)tree).getCost(u);
    }
}