تخيل لو كان بإمكانك فقط استخدام الخطوط المستقيمة والقطع الناقص والدوائر، ألن يكون من الصعب تصميم سيارة ذات خطوط ناعمة ومظهر معقد؟

في عام 1962، نشر المهندس الفرنسي بيير بيزييه منحنى بيزييه، والذي كان يستخدم في البداية لتصميم الجسم الرئيسي للسيارات.

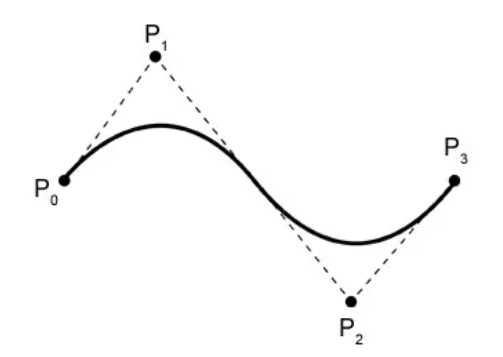
يمكن لمنحنيات بيزييه تحديد منحنى سلس من خلال سلسلة من نقاط التحكم. يمر المنحنى دائمًا عبر نقطتي التحكم الأولى والأخيرة ويتأثر بشكل نقاط التحكم الوسيطة. بالإضافة إلى ذلك، تتمتع منحنيات بيزييه بخاصية الهياكل المحدبة.

تستخدم منحنيات بيزييه على نطاق واسع في رسومات الكمبيوتر ونمذجة الصور، مثل الرسوم المتحركة وتصميم الخطوط والتصميم الصناعي.

صيغة

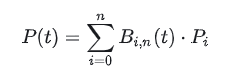
دعونا نفهم هذا.

P(t) يمثل نقطة على المنحنى عند t (t عبارة عن كسر بقيمة من 0 إلى 1). ما هي النقطة على المنحنى عند t؟ وصف المنحنى الشائع هو: y = f(x)، والآن دعونا نفهم P(t) كـ f(x). الفرق هو أن P(t) عبارة عن تمثيل حدودي (ونتيجة الحساب هي "متجه" مثل [x, y])، والذي سيتم شرحه بالتفصيل لاحقًا.

بعد ذلك، يمثل Pi نقطة التحكم i (i تبدأ من 0). بأخذ الشكل أعلاه كمثال، هناك 4 نقاط تحكم، وهي P0، P1، P2، P3. n في الصيغة هو الفهرس الأخير لنقاط التحكم، أي n = 3 (لاحظ أنه ليس عدد نقاط التحكم، بل العدد ناقص 1).

Bi,n(t) هي دالة أساس برنشتاين، والمعروفة أيضًا باسم الدالة الأساسية. لكل محدد (i، n)، هناك وظيفة أساسية مختلفة تتوافق معه. إذا فهمت من منظور مرجح، فيمكنك اعتبار الدالة الأساسية كدالة وزن، مما يشير إلى "مساهمة" نقطة التحكم i-th Pi في إحداثيات المنحنى عند موضع t.

صيغة الدالة الأساسية هي كما يلي:

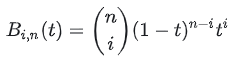
$n\genfrac{}{}{0px}{}{i}{}\backslash binom\{n\}\{i\}$( i n ​ ] هو رقم المجموعة (كم عدد الطرق لاختيار i من n؟). أما لماذا تبدو الدالة الأساسية هكذا، فيمكن فهمها فيما يتعلق بخوارزمية De Casteljau (انظر لاحقًا في النص) العودة إلى صيغة P(t)،

i

= $0{}_{\backslash sum\_\{i=0\}^\{n\}\mathrm{}\sum }^{}i=0$ n ​ هو رمز الجمع، مما يدل على أن الجزء اللاحق ( i ، n ($t){\cdot }_{PiB\_\{i,n\}(t)\; \backslash cdot\; P\_i}B{}_{}$(t )⋅Pi ) يجب جمعها من i=0 إلى i=n. بأخذ الشكل أعلاه كمثال، بافتراض أننا نريد حساب P(0.1)، كيف نفعل ذلك؟ ويتوسع على النحو التالي: عوض بـ t=0.1 لتحصل على: التمثيل البارامتري للمنحنى هنا يستشهد مباشرة بمقال من أحد مستخدمي الإنترنت (رابط) دعونا نركز على الصيغة أعلاه.

كما هو موضح في الشكل أعلاه، يمكن فهم الخط المستقيم الذي نعرفه من منظور آخر: باستخدام t (أي طول |AP| من النقطة P إلى النقطة المعروفة (x0,y0))، ومن ثم يمكن تحديد النقطة P من خلال الدوال المثلثية المذكورة أعلاه.

بشكل عام، يمكن كتابتها بالشكل التالي:

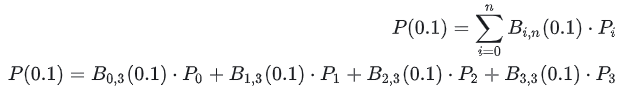
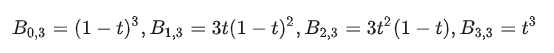هنا، P0 هو المتجه [x0,y0] و v هو أيضًا متجه. عند إضافتها معًا، يكون P(t) هو المتجه [x,y].

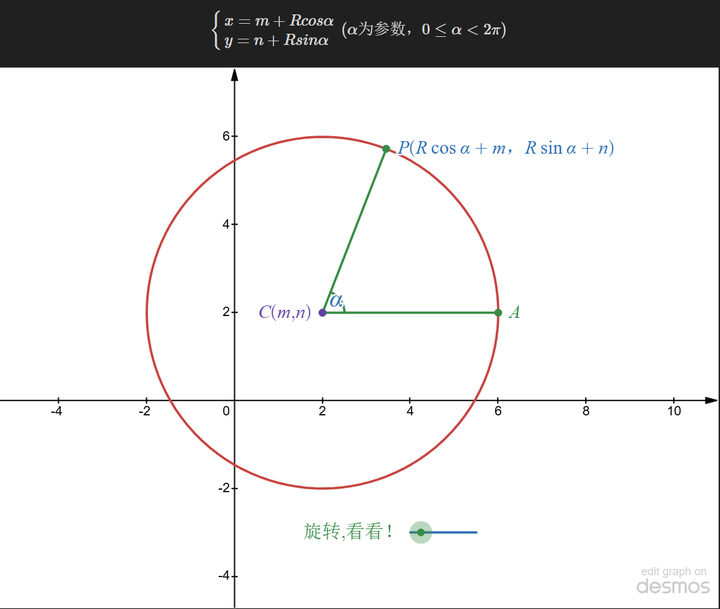
بالنظر إلى الدائرة مرة أخرى:

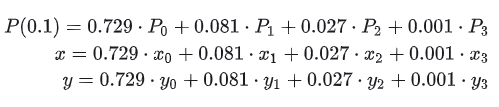
كما هو موضح في الرسم البياني، يمكن النظر إلى الدائرة على أنها ذات مركز معروف، مع تحديد أي نقطة على الدائرة بواسطة زاوية الدوران ونصف القطر. ويمكن كتابتها أيضًا بالشكل التالي:

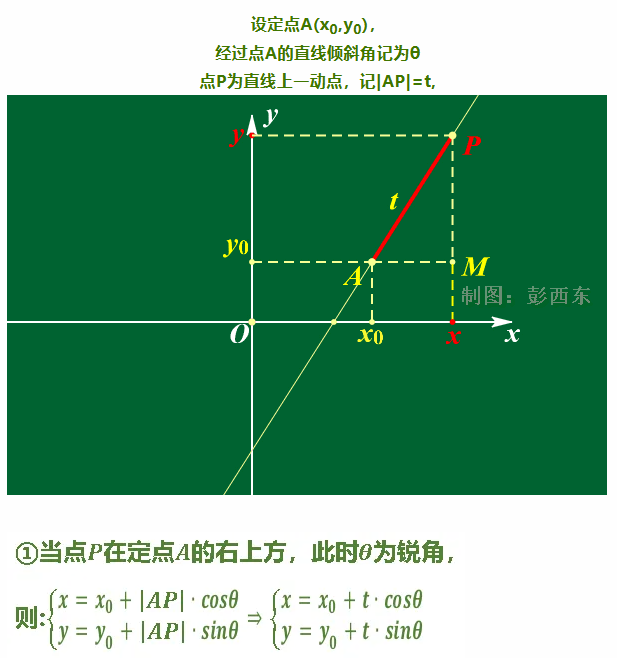تحافظ المعادلات البارامترية على الثبات الهندسي ويمكن أن تمثل أشكالًا مثل الدوائر (حيث يتوافق x واحد مع قيم y متعددة).

دي كاستلجاو

خوارزمية De Casteljau هي طريقة تستخدم في التطبيقات العملية لتقييم وتقريب منحنيات بيزييه للرسم والعمليات الأخرى. بالمقارنة مع طريقة التقييم السابقة القائمة على التعريف، فهي أسرع وأكثر استقرارا، وأقرب إلى خصائص منحنيات بيزييه.

ونشير هنا إلى مقالتين: link1 و link2

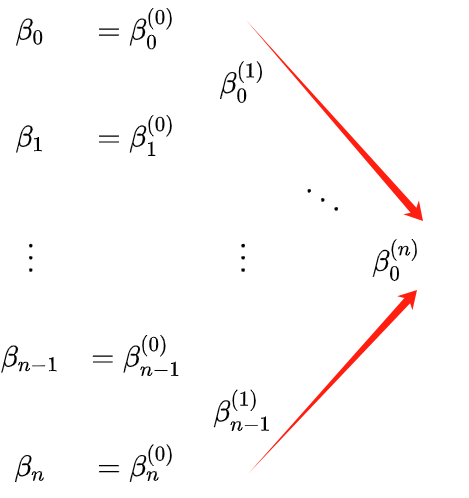
أولاً يتم تعريف ما يلي: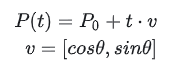

انظر إلى ما ورد أعلاه. إنه أمر مربك بعض الشيء مع الحروف المرتفعة والمنخفضة؛ يمكنك استخدام التكرار الثلاثي التالي لفهم:

الحواف الحمراء للمثلث في الشكل أعلاه هي نقاط التحكم للقطعتين مقسومتين على t0. لفهم t0 بشكل أكثر وضوحًا، P(t0) (أي،

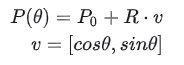
0

(

n

] &&&])

\beta_0^{(n)}

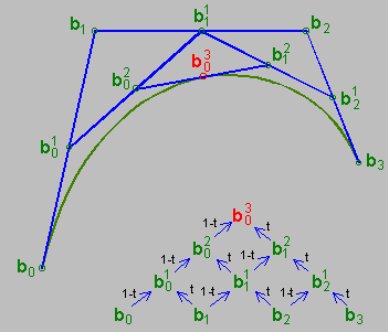
β] ]$0{}_{\mathrm{}}^{}$ )، نقاط التحكم في المنحنيين، يمكنك الرجوع إلى الشكل التالي: الشكل أعلاه يوضح العلاقات بين النقاط المختلفة عندما يكون t=0.5. من منظور "الاستيفاء"، يمكن أيضًا فهم عملية الحساب على النحو التالي: إيجاد نقاط المنتصف لكل زوج من نقاط التحكم المتجاورة (لأن t=0.5)، أي b01، b11، b21 (من فضلك اغفر لي التدوين؛ فالكتابة في LaTeX مزعجة للغاية) ابحث عن نقطة المنتصف b02 على b01−b11، وابحث عن نقطة المنتصف b12 على b11-b21 أوجد نقطة المنتصف b03 على b02−b12 ​ في الواقع، جوهر خوارزمية De Casteljau هو الاستيفاء والتكرار. رسم المنحنى على أساس De Casteljau حاليًا، يتم ملاحظة طريقتين. تتضمن إحدى الطرق اجتياز t من 0 إلى 1 بزيادات صغيرة (أي. 0.01). في كل مرة يتم البحث عن P(t)، يتم استخدام صيغة متكررة لتحديدها 0

(

n

] &&&])

\beta_0^{(n)}
β

]

]

0

${}_{\mathrm{}}^{}تطبيق$يبدو دائمًا أنه من غير الواقعي مجرد المشاهدة دون التدريب. لذلك كتبت كود التنفيذ الخاص بي لرسم المنحنى وقمت بتنظيمه في مجموعة أدوات: Compilelife's Toolkit الرمز الأساسي المقابل هنا