مقدمة 1

العملية التي تستدعي فيها الدالة نفسها تسمى العودية و
تسمى الوظيفة المقابلة وظيفة متكررة.
بما أن برمجة الكمبيوتر هي تطبيق أساسي للرياضيات، فلنفترض
نحاول أولاً أن نفهم المنطق الرياضي وراء التكرار.
بشكل عام، نحن جميعا ندرك مفهوم الوظائف. باختصار، الوظائف هي
المعادلات الرياضية التي تنتج مخرجات عند توفير المدخلات. على سبيل المثال:
لنفترض أن الدالة F(x) هي دالة معرفة بواسطة: F(x) = x^2 4
يمكننا كتابة كود Java لهذه الوظيفة على النحو التالي:

الكثافة السكانية الثابتة F(int x){
العودة (س * س 4)؛

الآن، يمكننا تمرير قيم مختلفة لـ x إلى هذه الوظيفة وتلقي مخرجاتنا
وفقاً لذلك.
قبل الانتقال إلى العودية، دعونا نحاول فهم رياضيات أخرى
المفهوم المعروف باسم مبدأ الاستقراء الرياضي (PMI).

مبدأ الاستقراء الرياضي (PMI) هو أسلوب لإثبات عبارة، أ
صيغة، أو نظرية يتم التأكيد عليها حول مجموعة من الأعداد الطبيعية. لديه
الخطوات الثلاث التالية:
1.** خطوة الحالة التافهة*: في هذه الخطوة سنثبت العبارة المطلوبة لـ
حالة أساسية مثل n = 0 أو n = 1.
2.* خطوة الافتراض**: في هذه الخطوة سنفترض أن العبارة المطلوبة
صالح لـ n = k.

1. لإثبات الخطوة: من نتائج خطوة الافتراض سنثبت أن، n = k 1 يكون صحيحًا أيضًا للمعادلة المطلوبة عندما يكون n = k صحيحًا.

على سبيل المثال: لنثبت باستخدام مبدأ الاستقراء الرياضي أن:
ق(ن): 1 2 3 ... ن = (ن * (ن 1))/2
(مجموع الأعداد الطبيعية N الأولى)
دليل:
الخطوة 1: بالنسبة لـ N = 1، S(1) = 1 صحيح.
الخطوة 2: افترض أن العبارة المعطاة صحيحة بالنسبة لـ N = k، أي
1 2 3 .... ك = (ك * (ك 1))/2
الخطوة 3: دعونا نثبت عبارة N = k 1 باستخدام الخطوة 2.

للإثبات: 1 2 3 ... (ك 1) = ((ك 1)*(ك 2))/2
دليل:

إضافة (k 1) إلى كل من LHS وRHS في النتيجة التي تم الحصول عليها في الخطوة 2:
1 2 3 ... (ك 1) = (ك*(ك 1))/2 (ك 1)

الآن، مع أخذ (k 1) المشترك من جانب RHS:
1 2 3 ... (ك 1) = (ك 1)*((ك 2)/2)

حسب القول الذي نحاول إثباته:
1 2 3 ... (ك 1) = ((ك 1)*(ك 2))/2
ومن هنا ثبت.

العمل بالتكرار

يمكننا تحديد خطوات النهج العودي من خلال تلخيص الخطوات الثلاثة المذكورة أعلاه
خطوات:
● الحالة الأساسية: يجب أن تحتوي الدالة العودية على شرط إنهاء حيث
ستتوقف العملية عن تسمية نفسها. تُعرف مثل هذه الحالة بالحالة الأساسية. بدون حالة أساسية، سيستمر في الاتصال بنفسه ويعلق في
حلقة لا نهائية. قريبًا، سيتم تجاوز عمق التكرار* وسيتم طرحه
خطأ.
● استدعاء متكرر: ستقوم الوظيفة العودية باستدعاء نفسها على إصدار أصغر
من المشكلة الرئيسية. يجب أن نكون حذرين أثناء كتابة هذه الخطوة كما هي
أمر بالغ الأهمية لمعرفة مشكلتك الأصغر بشكل صحيح.
● عملية حسابية صغيرة: بشكل عام، نقوم بإجراء خطوة حسابية في كل عملية تكرارية
يتصل. يمكننا تحقيق خطوة الحساب هذه قبل أو بعد المكالمة العودية
حسب طبيعة المشكلة.

ملاحظة : يستخدم Recursion مكدسًا مدمجًا يقوم بتخزين المكالمات العودية. وبالتالي، فإن
يجب أن يكون عدد المكالمات العودية صغيرًا قدر الإمكان لتجنب تجاوز سعة الذاكرة. لو
عدد مكالمات العودية يتجاوز الحد الأقصى المسموح به،
**عمق العودية** سيتم تجاوزه.
الآن، دعونا نرى كيفية حل بعض المشاكل الشائعة باستخدام Recursion

بيان المشكلة - البحث عن مضروب الرقم

المنهج: معرفة الخطوات الثلاث لمؤشر مديري المشتريات (PMI) ومن ثم ربطها باستخدام
العودية

1. الخطوة الاستقراءية: حساب مضروب الرقم n - F(n) الفرضية الاستقراءية: لقد حصلنا بالفعل على مضروب n-1 - F(n-1)
2. التعبير عن F(n) بدلالة F(n-1): F(n)=n*F(n-1). وهكذا نحصل على

حقيقة int العامة الثابتة (int n) {
int الجواب = حقيقة(ن-1); #خطوة الافتراض
عودة الجواب * ن؛ #حل المشكلة من خطوة الافتراض

1. الكود لم يكتمل بعد. الجزء المفقود هو الحالة الأساسية. الآن سوف نفعل ذلك التشغيل الجاف للعثور على الحالة التي يجب أن يتوقف فيها التكرار. خذ بعين الاعتبار n = 5:

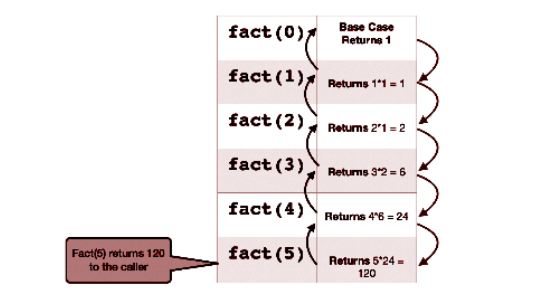
كما نرى أعلاه، نحن نعرف بالفعل إجابة n = 0، وهي 1. لذلك سنقوم
احتفظ بهذا كحالتنا الأساسية. ومن ثم يصبح الكود الآن:

عامل int الثابت العام (int n) {
إذا (ن == 0) // الحالة الأساسية
العودة 1؛
آخر
إرجاع n*factorial(n-1); // حالة متكررة