إلى أي مدى يمكنك تحسين برنامج لحساب تسلسل فيبوناتشي؟

مقدمة

عندما كنت أتعلم لغة بايثون، أعطانا معلمنا واجبًا منزليًا -- حساب العدد النوني من تسلسل فيبوناتشي.

أعتقد أن الأمر سهل جدًا، لذا أكتب هذا الكود:

def fib(n):
    if n == 0:
        return 0
    elif n == 1:
        return 1
    else:
        return fib(n - 1)   fib(n - 2)

لاحقًا، أدركت أن هذا النوع من الحلول يكلف الكثير من الوقت.

تحسين البرنامج

أقوم بتغيير الحل إلى التكرار.

def fib(n):
    ls = [1,1]
    for i in range(2,n):
        ls.append(ls[i-1] ls[i-2])

    return ls[n-1]

أستخدم matplotlib لرسم الوقت الذي يكلفه:

import time
import matplotlib.pyplot as plt


def bench_mark(func, *args):
    # calculate the time
    start = time.perf_counter()
    result = func(*args)
    end = time.perf_counter()

    return end - start, result  # return the time and the result

def fib(n):
    ls = [1,1]
    for i in range(2,n):
        ls.append(ls[i-1] ls[i-2])

    return ls[n-1]

mark_list = []

for i in range(1,10000):
    mark = bench_mark(fib,i)
    mark_list.append(mark[0])
    print(f"size : {i} , time : {mark[0]}")

plt.plot(range(1, 10000), mark_list)
plt.xlabel('Input Size')
plt.ylabel('Execution Time (seconds)')
plt.title('Test fot fibonacci')
plt.grid(True)
plt.show()

النتيجة هنا:

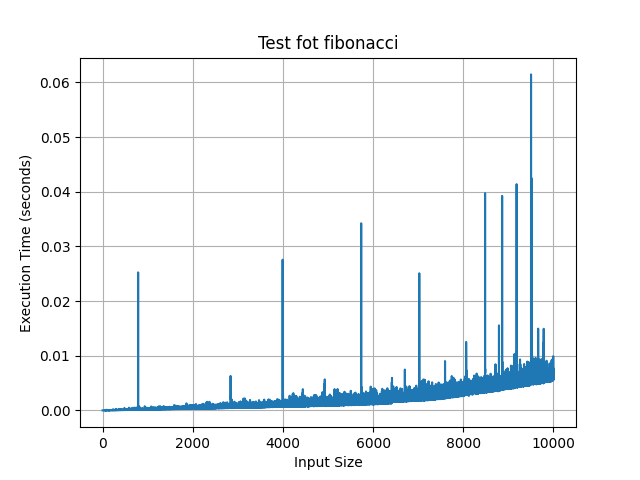
الوقت الذي تستغرقه قصير جدًا.

لكنني أكتب أكذوبة (300000)، بتكلفة 5.719049899998936 ثانية. إنه طويل أكثر من اللازم.

عندما أكبر، أتعلم ذاكرة التخزين المؤقت، لذلك أقوم بتغيير الحل لاستخدام الإملاء لتخزين النتيجة.

from functools import lru_cache
@lru_cache(maxsize=None)
def fib(n):
    if n 



أو يمكننا كتابة ذاكرة التخزين المؤقت بأنفسنا.


def fib(n, cache={}):
    if n in cache:
        return cache[n]
    elif n