ك-أقرب انحدار الجيران

انحدار k-أقرب الجيران (k-NN) هو طريقة غير معلمية تتنبأ بقيمة الإخراج بناءً على المتوسط ​​(أو المتوسط ​​المرجح) لأقرب نقاط بيانات التدريب k في مساحة الميزة. يمكن لهذا النهج أن يصمم بشكل فعال العلاقات المعقدة في البيانات دون افتراض نموذج وظيفي محدد.

يمكن تلخيص طريقة الانحدار k-NN على النحو التالي:

1. قياس المسافة: تستخدم الخوارزمية مقياس المسافة (المسافة الإقليدية عادةً) لتحديد "القرب" من نقاط البيانات.
2. k Neighbors: تحدد المعلمة k عدد الجيران الأقرب الذين يجب مراعاتهم عند إجراء التنبؤات.
3. التنبؤ: القيمة المتوقعة لنقطة بيانات جديدة هي متوسط ​​قيم أقرب جيرانها.

المفاهيم الأساسية

1. غير بارامترية : على عكس النماذج البارامترية، لا تفترض k-NN نموذجًا محددًا للعلاقة الأساسية بين ميزات الإدخال والمتغير المستهدف. وهذا يجعلها مرنة في التقاط الأنماط المعقدة.

2. حساب المسافة: يمكن أن يؤثر اختيار مقياس المسافة بشكل كبير على أداء النموذج. تشمل المقاييس الشائعة المسافات الإقليدية ومانهاتن ومينكوفسكي.

3. اختيار k: يمكن اختيار عدد الجيران (k) بناءً على التحقق المتبادل. يمكن أن يؤدي الحرف k الصغير إلى الإفراط في التجهيز، في حين أن الحرف k الكبير يمكن أن يؤدي إلى تسهيل التنبؤ أكثر من اللازم، ومن المحتمل أن يؤدي إلى نقص التجهيز.

ك-أقرب مثال على انحدار الجيران

يوضح هذا المثال كيفية استخدام انحدار k-NN مع ميزات متعددة الحدود لنمذجة العلاقات المعقدة مع الاستفادة من الطبيعة غير البارامترية لـ k-NN.

مثال كود بايثون

1. استيراد المكتبات

import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import PolynomialFeatures
from sklearn.neighbors import KNeighborsRegressor
from sklearn.metrics import mean_squared_error, r2_score

تستورد هذه الكتلة المكتبات اللازمة لمعالجة البيانات والتخطيط والتعلم الآلي.

2. إنشاء بيانات نموذجية

np.random.seed(42)  # For reproducibility
X = np.linspace(0, 10, 100).reshape(-1, 1)
y = 3 * X.ravel()   np.sin(2 * X.ravel()) * 5   np.random.normal(0, 1, 100)

تقوم هذه الكتلة بإنشاء بيانات نموذجية تمثل علاقة مع بعض الضوضاء، ومحاكاة اختلافات البيانات في العالم الحقيقي.

3. تقسيم مجموعة البيانات

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

تقسم هذه الكتلة مجموعة البيانات إلى مجموعات تدريب واختبار لتقييم النموذج.

4. إنشاء ميزات متعددة الحدود

degree = 3  # Change this value for different polynomial degrees
poly = PolynomialFeatures(degree=degree)
X_poly_train = poly.fit_transform(X_train)
X_poly_test = poly.transform(X_test)

تنشئ هذه الكتلة ميزات متعددة الحدود من مجموعات بيانات التدريب والاختبار، مما يسمح للنموذج بالتقاط العلاقات غير الخطية.

5. إنشاء وتدريب نموذج الانحدار k-NN

k = 5  # Number of neighbors
knn_model = KNeighborsRegressor(n_neighbors=k)
knn_model.fit(X_poly_train, y_train)

تقوم هذه الكتلة بتهيئة نموذج الانحدار k-NN وتدريبه باستخدام الميزات متعددة الحدود المستمدة من مجموعة بيانات التدريب.

6. توقع التنبؤات

y_pred = knn_model.predict(X_poly_test)

تستخدم هذه الكتلة النموذج المُدرب لإجراء تنبؤات على مجموعة الاختبار.

7. رسم النتائج

plt.figure(figsize=(10, 6))
plt.scatter(X, y, color='blue', alpha=0.5, label='Data Points')
X_grid = np.linspace(0, 10, 1000).reshape(-1, 1)
X_poly_grid = poly.transform(X_grid)
y_grid = knn_model.predict(X_poly_grid)
plt.plot(X_grid, y_grid, color='red', linewidth=2, label=f'k-NN Regression (k={k}, Degree {degree})')
plt.title(f'k-NN Regression (Polynomial Degree {degree})')
plt.xlabel('X')
plt.ylabel('Y')
plt.legend()
plt.grid(True)
plt.show()

تنشئ هذه الكتلة مخططًا مبعثرًا لنقاط البيانات الفعلية مقابل القيم المتوقعة من نموذج الانحدار k-NN، مما يؤدي إلى تصور المنحنى المناسب.

الإخراج بـ k = 1:

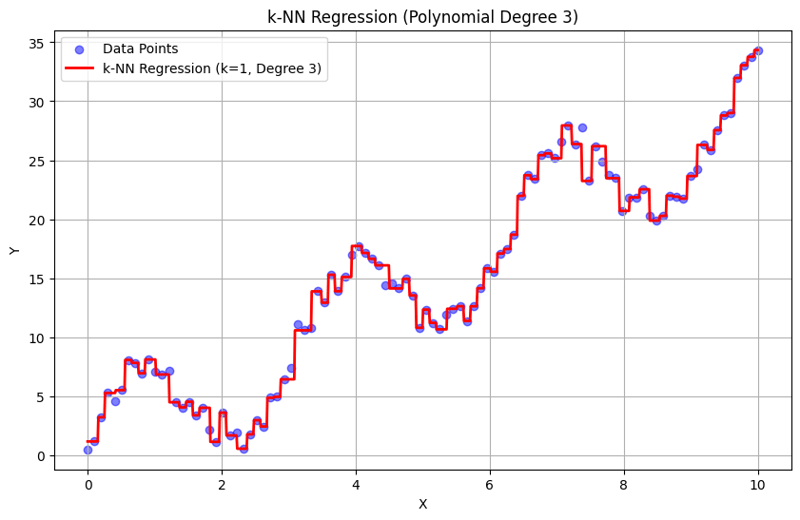
الإخراج بـ k = 10:

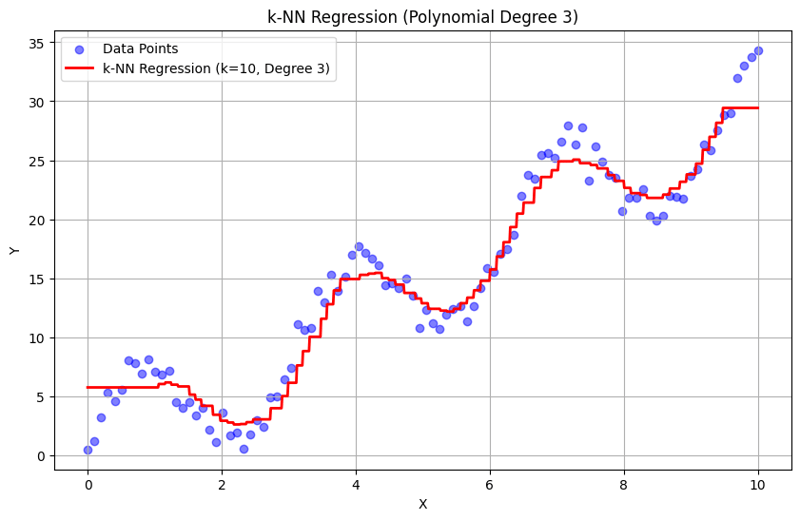
يوضح هذا النهج المنظم كيفية تنفيذ وتقييم انحدار k-Nearest Neighbors مع ميزات متعددة الحدود. من خلال التقاط الأنماط المحلية من خلال حساب متوسط ​​استجابات الجيران القريبين، يقوم انحدار k-NN بنمذجة العلاقات المعقدة في البيانات بشكل فعال مع توفير تنفيذ مباشر. يؤثر اختيار k ودرجة متعددة الحدود بشكل كبير على أداء النموذج ومرونته في التقاط الاتجاهات الأساسية.