بما أننا تحدثنا عن خوارزميات الفرز المختلفة، سنتعرف اليوم على خوارزمية الفرز بالاختيار. خوارزمية فرز تسمح بأقل قدر ممكن من عمليات المبادلة في بيئة محدودة الذاكرة.

جدول المحتويات

1. مقدمة
2. ما هي خوارزمية الفرز بالتحديد؟
3. كيف يعمل فرز التحديد؟
   • تعقيد الوقت
   • تعقيد الفضاء
4. التنفيذ في جافا سكريبت
5. حل مشاكل LeetCode
6. خاتمة

مقدمة

فرز التحديد هو خوارزمية فرز بسيطة وفعالة تعمل عن طريق تحديد العنصر الأصغر (أو الأكبر) بشكل متكرر من الجزء غير المصنف من القائمة ونقله إلى بداية (أو نهاية) الجزء الذي تم فرزه. تتكرر هذه العملية حتى يتم فرز القائمة بأكملها. في هذه المقالة، سوف نتعمق في تفاصيل خوارزمية الفرز بالاختيار، وتنفيذها في JavaScript، وتطبيقاتها في حل المشكلات الواقعية.

ما هي خوارزمية فرز التحديد؟

خوارزمية فرز التحديد هي خوارزمية فرز مقارنة موضعية. يقسم قائمة الإدخال إلى قسمين:

1. الجزء المرتب في الطرف الأيسر
2. الجزء غير المصنف في الطرف الأيمن

تقوم الخوارزمية بشكل متكرر باختيار أصغر عنصر من الجزء غير المصنف وتبديله بالعنصر غير المصنف في أقصى اليسار، مما يؤدي إلى تحريك الحدود بين الأجزاء المصنفة وغير المصنفة عنصرًا واحدًا إلى اليمين.

كيف يعمل فرز التحديد؟

دعونا نستعرض مثالًا باستخدام المصفوفة [64، 25، 12، 22، 11]:

1. الصفيف الأولي: [64، 25، 12، 22، 11]

• الجزء المصنف: []
• الجزء غير المفرز: [64، 25، 12، 22، 11]

1. التمريرة الأولى:

• ابحث عن الحد الأدنى في الجزء غير المصنف: 11
• مبادلة 11 بالعنصر الأول غير المصنف (64)
• النتيجة: [11، 25، 12، 22، 64]
• الجزء المرتب: [11]
• الجزء غير المفرز: [25، 12، 22، 64]

1. التمريرة الثانية:

• ابحث عن الحد الأدنى في الجزء غير المصنف: 12
• مبادلة 12 بالعنصر الأول غير المصنف (25)
• النتيجة: [11، 12، 25، 22، 64]
• الجزء المرتب: [11، 12]
• الجزء غير المصنف: [25، 22، 64]

1. التمريرة الثالثة:

• ابحث عن الحد الأدنى في الجزء غير المصنف: 22
• مبادلة 22 بالعنصر الأول غير المصنف (25)
• النتيجة: [11، 12، 22، 25، 64]
• الجزء المرتب: [11، 12، 22]
• الجزء غير المصنف: [25، 64]

1. التمريرة الرابعة:

• ابحث عن الحد الأدنى في الجزء غير المصنف: 25
• 25 موجود بالفعل في الموضع الصحيح
• النتيجة: [11، 12، 22، 25، 64]
• الجزء المرتب: [11، 12، 22، 25]
• الجزء غير المصنف: [64]

1. التمريرة النهائية:
   • يتبقى عنصر واحد فقط، وهو في الموضع الصحيح تلقائيًا
   • النتيجة النهائية: [11، 12، 22، 25، 64]

تم الآن فرز المصفوفة بالكامل.

تعقيد الوقت

يحتوي فرز التحديد على تعقيد زمني قدره O(n^2) في جميع الحالات (الأفضل، المتوسط، والأسوأ)، حيث n هو عدد العناصر في المصفوفة. وذلك بسبب:

• الحلقة الخارجية تعمل n-1 مرة
• لكل تكرار للحلقة الخارجية، تعمل الحلقة الداخلية n-i-1 مرات (حيث i هو التكرار الحالي للحلقة الخارجية)

ينتج عن هذا تقريبًا (n^2)/2 مقارنات ومقايضات n، والتي يتم تبسيطها إلى O(n^2).

نظرًا لهذا التعقيد الزمني التربيعي، فإن فرز التحديد ليس فعالاً لمجموعات البيانات الكبيرة. ومع ذلك، فإن بساطته وحقيقة أنه يقوم بأقل عدد ممكن من عمليات المبادلة يمكن أن يجعله مفيدًا في مواقف معينة، خاصة عندما تكون الذاكرة المساعدة محدودة.

تعقيد الفضاء

يحتوي فرز التحديد على تعقيد مساحة يبلغ O(1) لأنه يقوم بفرز المصفوفة في مكانها. فهو يتطلب فقط قدرًا ثابتًا من مساحة الذاكرة الإضافية بغض النظر عن حجم الإدخال. وهذا يجعلها فعالة في الذاكرة، وهو ما يمكن أن يكون مفيدًا في البيئات ذات الذاكرة المحدودة.

التنفيذ في جافا سكريبت

إليك تطبيق JavaScript لخوارزمية فرز التحديد:

function selectionSort(arr) {
  const n = arr.length;

  for (let i = 0; i 


دعونا نحلل الكود:

نحدد اختيارًا للوظيفة، وفرزًا يأخذ مصفوفة كمدخل.
نقوم بالتكرار عبر المصفوفة باستخدام الحلقة الخارجية (i)، والتي تمثل الحدود بين الأجزاء المصنفة وغير المصنفة.
لكل تكرار، نفترض أن العنصر الأول الذي لم يتم فرزه هو الحد الأدنى ونقوم بتخزين فهرسه.
نستخدم بعد ذلك الحلقة الداخلية (j) للعثور على الحد الأدنى الفعلي للعنصر في الجزء غير المصنف.
إذا وجدنا عنصرًا أصغر، نقوم بتحديث minIndex.
بعد العثور على الحد الأدنى، نقوم بتبديله بالعنصر الأول غير المصنف إذا لزم الأمر.
نكرر هذه العملية حتى يتم فرز المصفوفة بأكملها.

  
  
  حل مشاكل LeetCode


دعونا نحل مشكلة خوارزمية leetcode باستخدام خوارزمية الفرز بالاختيار. هلا فعلنا؟

  
  
  المشكلة: فرز مصفوفة [متوسطة]


المشكلة: بالنظر إلى مجموعة من الأعداد الصحيحة، قم بفرز المصفوفة بترتيب تصاعدي وإعادتها. يجب عليك حل المشكلة دون استخدام أي وظائف مضمنة في التعقيد الزمني O(nlog(n)) وبأقل تعقيد ممكن للمساحة.

المنهج:: لحل هذه المشكلة، يمكننا تطبيق خوارزمية فرز التحديد مباشرة. يتضمن ذلك التكرار عبر المصفوفة، والعثور على أصغر عنصر في الجزء غير المصنف، واستبداله بالعنصر الأول غير المصنف. نكرر هذه العملية حتى يتم فرز المصفوفة بأكملها.

حل:

// This function sorts an array of integers in ascending order using the Selection Sort algorithm.
const sortArray = function (nums) {
  // Get the length of the input array.
  const n = nums.length;

  // Iterate through the array, starting from the first element.
  for (let i = 0; i 


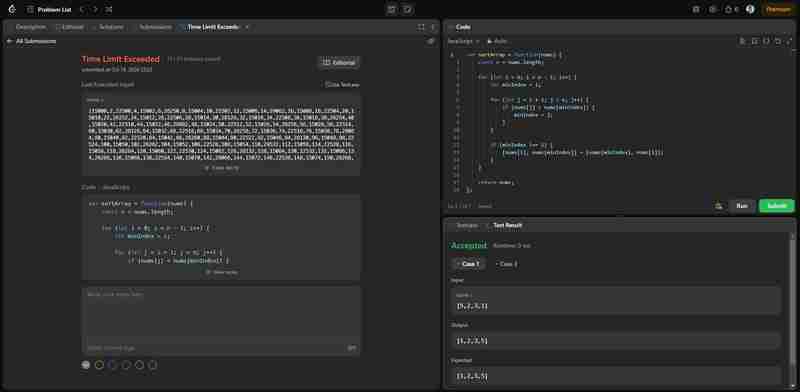
 يطبق هذا الحل مباشرة خوارزمية فرز التحديد التي قمنا بتنفيذها مسبقًا. على الرغم من أنه يحل المشكلة بشكل صحيح، تجدر الإشارة إلى أن هذا الحل قد يتجاوز الحد الزمني للمدخلات الكبيرة في LeetCode بسبب التعقيد الزمني O(n^2) لفرز التحديد. الصورة أدناه توضح أن الحل صحيح ولكنه غير فعال.



  
  
  خاتمة


 في الختام، يعد Selection Sort خوارزمية فرز بسيطة وبديهية تعمل كمقدمة ممتازة لعالم تقنيات الفرز. بساطته تجعل من السهل فهمه وتنفيذه، مما يجعله أداة تعليمية قيمة للمبتدئين. ومع ذلك، نظرًا لتعقيدها الزمني التربيعي O(n^2)، فهي غير فعالة لمجموعات البيانات الكبيرة. بالنسبة لمجموعات البيانات الكبيرة أو التطبيقات المهمة للأداء، يفضل استخدام خوارزميات أكثر كفاءة مثل QuickSort أو MergeSort أو وظائف الفرز المضمنة.


  
  
  ابق على اطلاع دائم ومتصل


لضمان عدم تفويت أي جزء من هذه السلسلة وللتواصل معي لمزيد من التعمق

مناقشات حول تطوير البرمجيات (الويب، الخادم، الهاتف المحمول أو الاستخلاص/الأتمتة)، البيانات

الهياكل والخوارزميات، وغيرها من المواضيع التقنية المثيرة، تابعني على:



    
      

        
    
  

    

الحل العظيم؟متابعة

    

      مهندس برمجيات | الكاتب الفني | مطور الواجهة الخلفية والويب والجوال؟ | شغوف بصياغة حلول برمجية فعالة وقابلة للتطوير. #لنتواصل ؟
    
  

• جيت هاب
• لينكد إن
• X (تويتر)

ترقبوا البرمجة وسعيدة ‍؟؟