يمكن حل العديد من مشاكل العالم الحقيقي باستخدام خوارزميات الرسم البياني. الرسوم البيانية مفيدة في النمذجة وحل مشاكل العالم الحقيقي. على سبيل المثال، يمكن صياغة مشكلة العثور على أقل عدد من الرحلات الجوية بين مدينتين باستخدام رسم بياني، حيث تمثل القمم المدن وتمثل الحواف الرحلات الجوية بين مدينتين متجاورتين، كما هو موضح في الشكل أدناه. مشكلة العثور على أقل عدد ممكن من الرحلات المتصلة
بين مدينتين يتم تقليله إلى إيجاد أقصر مسار بين قمتين في الرسم البياني.

تعرف دراسة مسائل الرسوم البيانية بـ نظرية الرسم البياني. تأسست نظرية الرسم البياني على يد ليونارد أويلر في عام 1736، عندما قدم مصطلحات الرسم البياني لحل مشكلة جسور كونيجسبيرج السبعة الشهيرة. مدينة كونيغسبيرغ، بروسيا (كالينينغراد حالياً، روسيا)، تم تقسيمها بواسطة نهر بريجيل. كانت هناك جزيرتان على النهر. تم ربط المدينة والجزر بسبعة جسور، كما هو موضح في الشكل أدناه (أ). والسؤال هو: هل يمكن للمرء أن يمشي ويعبر كل جسر مرة واحدة بالضبط ثم يعود إلى نقطة البداية؟ أثبت أويلر أن ذلك غير ممكن.

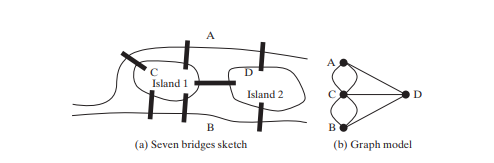
لإثبات الدليل، قام أويلر أولاً بتجريد خريطة مدينة كونيجسبيرج عن طريق إزالة جميع الشوارع، وإنتاج المخطط الموضح في الشكل أعلاه (أ). بعد ذلك، استبدل كل كتلة أرضية بنقطة، تسمى قمة أو عقدة، وكل جسر بخط يسمى حافة، كما هو موضح في الشكل أعلاه (ب). يُطلق على هذا الهيكل ذو القمم والحواف اسم الرسم البياني.

بالنظر إلى الرسم البياني، نتساءل عما إذا كان هناك مسار يبدأ من أي قمة، ويمر بجميع الحواف مرة واحدة بالضبط، ويعود إلى قمة البداية. أثبت أويلر أنه لكي يوجد مثل هذا المسار، يجب أن يكون لكل قمة عدد زوجي من الحواف. ولذلك فإن مشكلة جسور كونيجسبيرج السبعة ليس لها حل.

غالبًا ما يتم حل مشكلات الرسم البياني باستخدام الخوارزميات. لخوارزميات الرسم البياني العديد من التطبيقات في مجالات مختلفة، مثل علوم الكمبيوتر والرياضيات وعلم الأحياء والهندسة والاقتصاد وعلم الوراثة والعلوم الاجتماعية.

مصطلحات الرسم البياني الأساسية

يتكون الرسم البياني من القمم والحواف التي تربط القمم. لا يفترض هذا الفصل أن لديك أي معرفة مسبقة بنظرية الرسم البياني أو الرياضيات المنفصلة. نحن نستخدم مصطلحات واضحة وبسيطة لتعريف الرسوم البيانية.

ما هو الرسم البياني؟ الرسم البياني هو هيكل رياضي يمثل العلاقات بين الكيانات في العالم الحقيقي. على سبيل المثال، يمثل الرسم البياني في الشكل أعلاه الرحلات الجوية بين المدن، ويمثل الرسم البياني في الشكل أدناه (ب) الجسور بين الكتل الأرضية.

يتكون الرسم البياني من مجموعة غير فارغة من القمم (المعروفة أيضًا بالعقد أو النقاط)، ومجموعة من الحواف التي تربط القمم. لتسهيل الأمر، نحدد الرسم البياني على أنه G = (V, E)، حيث تمثل V مجموعة من القمم وE تمثل مجموعة من الحواف. على سبيل المثال، V وE للرسم البياني في الشكل أدناه هما كما يلي:

V = {"سياتل"، "سان فرانسيسكو"، "لوس أنجلوس"،
"دنفر"، "كانساس سيتي"، "شيكاغو"، "بوسطن"، "نيويورك"،
"أتلانتا"، "ميامي"، "دالاس"، "هيوستن"}؛

E = {{"سياتل"، "سان فرانسيسكو"}،{"سياتل"، "شيكاغو"}،
{"سياتل"، "دنفر"}، {"سان فرانسيسكو"، "دنفر"}،
...
};

قد يكون الرسم البياني موجهًا أو غير موجه. في الرسم البياني الموجه، كل حافة لها اتجاه، مما يشير إلى أنه يمكنك الانتقال من قمة إلى أخرى عبر الحافة. يمكنك نموذج العلاقات بين الوالدين والطفل باستخدام رسم بياني موجه، حيث تشير الحافة من الرأس A إلى B إلى أن A هو أصل B. ويبين الشكل أدناه (أ) رسمًا بيانيًا موجهًا.

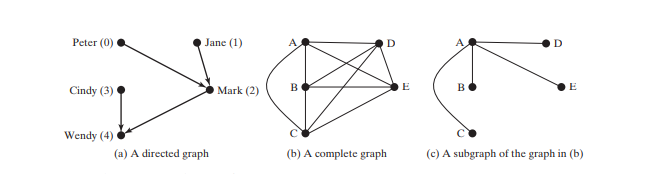
في الرسم البياني غير الموجه، يمكنك التحرك في كلا الاتجاهين بين القمم. الرسم البياني في الشكل أدناه غير موجه.

قد تكون الحواف مرجحة أو غير مرجحة. على سبيل المثال، يمكنك تعيين وزن لكل حافة في الرسم البياني في الشكل أعلاه للإشارة إلى وقت الرحلة بين المدينتين.

يقال أن الرأسين في الرسم البياني هما متجاوران إذا كانا متصلين بنفس الحافة. وبالمثل، يقال أن الحافتين متجاورتان إذا كانتا متصلتين بنفس الرأس. يقال إن الحافة في الرسم البياني التي تربط بين رأسين هي حادثة لكلا الرأسين. درجة للرأس هي عدد الحواف الواردة إليه.

يسمى الرأسان جيرانًا إذا كانا متجاورين. وبالمثل، يطلق على الحافتين اسم جيران إذا كانا متجاورين.

الحلقة هي حافة تربط قمة بنفسها. إذا كان رأسان متصلان بحافتين أو أكثر، تسمى هذه الحواف حواف متوازية. الرسم البياني البسيط هو الذي لا يحتوي على أي حلقات أو حواف متوازية. في الرسم البياني الكامل، كل زوجين من القمم متصلان، كما هو موضح في الشكل أدناه (ب).

الرسم البياني يكون متصلًا إذا كان هناك مسار بين أي رأسين في الرسم البياني. الرسم البياني الرسم البياني الفرعي للرسم البياني G هو رسم بياني تكون مجموعة رؤوسه مجموعة فرعية من مجموعة G ومجموعة حوافه هي مجموعة فرعية من مجموعة G. على سبيل المثال، الرسم البياني في الشكل أعلاه (ج) هو رسم بياني فرعي للرسم البياني في الشكل أعلاه (ب).

افترض أن الرسم البياني متصل وغير موجه. الدورة هي مسار مغلق يبدأ من قمة وينتهي عند نفس الرأس. الرسم البياني المتصل هو شجرة إذا لم يكن به دورات. الشجرة الممتدة للرسم البياني G هي رسم بياني فرعي متصل من G والرسم البياني الفرعي عبارة عن شجرة تحتوي على جميع القمم في G.