يقدم هذا القسم عدة أمثلة لتحديد Big O لبيانات التكرار والتسلسل والاختيار.

مثال 1

خذ بعين الاعتبار التعقيد الزمني للحلقة التالية:

لـ (int i = 1; i ك = ك 5؛

إنه وقت ثابت، c، للتنفيذ

ك = ك 5؛

بما أن الحلقة يتم تنفيذها n مرات، فإن التعقيد الزمني للحلقة هو

T(n) = (ثابت ج)*n = O(n).

التحليل النظري يتنبأ بأداء الخوارزمية. لمعرفة كيفية أداء هذه الخوارزمية، نقوم بتشغيل التعليمات البرمجية في البرنامج أدناه للحصول على وقت التنفيذ لـ n = 1000000، 10000000، 100000000، و100000000.

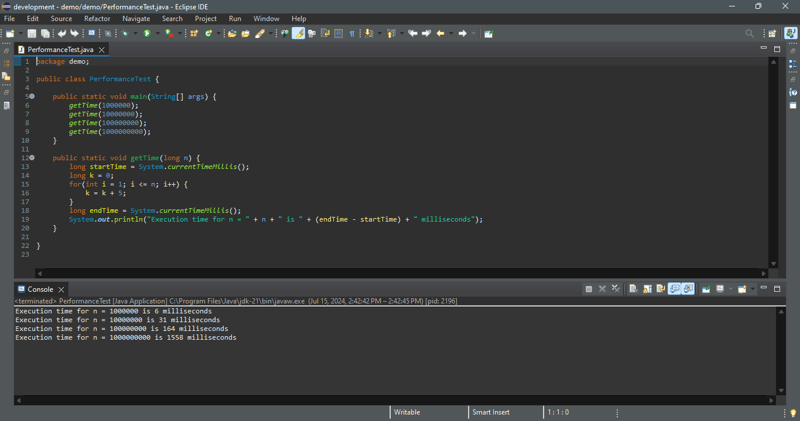
يتوقع تحليلنا تعقيدًا زمنيًا خطيًا لهذه الحلقة. كما هو موضح في عينة الإخراج، عندما يزيد حجم الإدخال 10 مرات، يزيد وقت التشغيل 10 مرات تقريبًا. التنفيذ يؤكد التنبؤ.

مثال 2

ما هو التعقيد الزمني للحلقة التالية؟

لـ (int i = 1; i لـ (int j = 1; j ك = ك ط ي؛

إنه وقت ثابت، c، للتنفيذ

ك = ك ط ي؛

يتم تنفيذ الحلقة الخارجية n مرات. لكل تكرار في الحلقة الخارجية، يتم تنفيذ الحلقة الداخلية n مرات. وبالتالي فإن التعقيد الزمني للحلقة هو

T(n) = (ثابت ج)*n*n = O(n^2)

الخوارزمية ذات التعقيد الزمني O(n^2) تسمى الخوارزمية التربيعية وتظهر معدل نمو تربيعي. تنمو الخوارزمية التربيعية بسرعة مع زيادة حجم المشكلة. إذا قمت بمضاعفة حجم الإدخال، فسيتم مضاعفة وقت الخوارزمية أربع مرات. غالبًا ما تكون الخوارزميات ذات الحلقة المتداخلة من الدرجة الثانية.

مثال 3

خذ بعين الاعتبار الحلقة التالية:

لـ (int i = 1; i لـ (int j = 1; j ك = ك ط ي؛

يتم تنفيذ الحلقة الخارجية n مرات. بالنسبة إلى i = 1, 2, c، يتم تنفيذ الحلقة الداخلية مرة واحدة ومرتين وn مرات. وبالتالي فإن التعقيد الزمني للحلقة هو

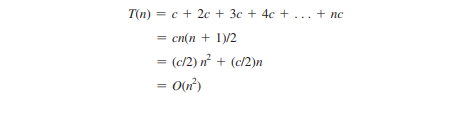
مثال 4

خذ بعين الاعتبار الحلقة التالية:

لـ (int i = 1; i لـ (int j = 1; j ك = ك ط ي؛

يتم تنفيذ الحلقة الداخلية 20 مرة، والحلقة الخارجية n مرة. وبالتالي فإن التعقيد الزمني للحلقة هو

T(n) = 20*c*n = O(n)

مثال 5

ضع في اعتبارك التسلسل التالي:

لـ (int j = 1; j ك = ك 4؛

لـ (int i = 1; i لـ (int j = 1; j ك = ك ط ي؛

يتم تنفيذ الحلقة الأولى 10 مرات، والحلقة الثانية 20 * ن مرة. وبالتالي فإن التعقيد الزمني للحلقة هو

T(n) = 10*ج 20*ج*ن = O(n)

مثال 6

خذ بعين الاعتبار بيان الاختيار التالي:

إذا (list.contains(e)) {
System.out.println(e);

آخر
لـ (الكائن ر: القائمة) {
System.out.println(t);

لنفترض أن القائمة تحتوي على عناصر n. وقت تنفيذ list.contains(e) هو O(n). تستغرق الحلقة في جملة else وقتًا O(n). ومن ثم، فإن التعقيد الزمني للبيان بأكمله هو

مثال 7

خذ بعين الاعتبار حساب a^n لعدد صحيح n. يمكن لخوارزمية بسيطة أن تضرب عدد n من المرات، كما يلي:

النتيجة = 1؛
لـ (int i = 1; i النتيجة *= أ;

تستغرق الخوارزمية وقتًا O(n). دون فقدان العمومية، افترض أن n = 2^k. يمكنك تحسين الخوارزمية باستخدام المخطط التالي:

النتيجة = أ;
لـ (int i = 1; i النتيجة = النتيجة * النتيجة؛

تستغرق الخوارزمية وقتًا (تسجيل الدخول). بالنسبة لـ n التعسفي، يمكنك مراجعة الخوارزمية وإثبات أن التعقيد لا يزال O(logn).

للتبسيط، نظرًا لأن 0(logn) = 0(log2n) = 0(logan)، فقد تم حذف الأساس الثابت.