يبدأ بحث العمق الأول للرسم البياني من قمة في الرسم البياني ويزور جميع القمم في الرسم البياني إلى أقصى حد ممكن قبل التراجع.
يشبه بحث العمق الأول للرسم البياني بحث العمق الأول لشجرة تمت مناقشتها في اجتياز الشجرة، اجتياز الشجرة. وفي حالة الشجرة، يبدأ البحث من الجذر. في الرسم البياني، يمكن أن يبدأ البحث من أي قمة.

يقوم البحث العميق الأول للشجرة بزيارة الجذر أولاً، ثم يزور بشكل متكرر الأشجار الفرعية للجذر. وبالمثل، فإن البحث عن العمق أولاً في الرسم البياني يزور القمة أولاً، ثم يزور بشكل متكرر جميع القمم المجاورة لتلك القمة. والفرق هو أن الرسم البياني قد يحتوي على دورات، مما قد يؤدي إلى تكرار لا نهائي. لتجنب هذه المشكلة، تحتاج إلى تتبع القمم التي تمت زيارتها بالفعل.

يسمى البحث العمق أولاً لأنه يبحث "أعمق" في الرسم البياني قدر الإمكان. يبدأ البحث من بعض القمم v. بعد زيارة v، فإنه يزور جارًا غير مرغوب فيه لـ v. إذا لم يكن لدى v جارًا غير مرغوب فيه، فإن البحث يتراجع إلى القمة التي وصل منها v. نفترض أن الرسم البياني متصل ويبدأ البحث من أي قمة يمكن أن تصل إلى جميع القمم.

خوارزمية البحث العمق الأول

تم وصف خوارزمية البحث المتعمق أولاً في الكود أدناه.

الإدخال: G = (V، E) وقمة البداية v
الإخراج: شجرة DFS متجذرة في v
1 شجرة dfs(قمة الرأس v) {
2 زيارة ضد؛
3 لكل جار ث
4 إذا (لم تتم زيارته) {
5 قم بتعيين v كأصل لـ w في الشجرة؛
6 دفس(ث);
7
8

يمكنك استخدام مصفوفة باسم isVisited للإشارة إلى ما إذا كان قد تمت زيارة قمة ما. في البداية، isVisited[i] هو خطأ لكل قمة i. بمجرد زيارة قمة، مثل v، يتم تعيين isVisited[v] على true.

تأمل الرسم البياني في الشكل أدناه (أ). لنفترض أننا بدأنا بحث العمق أولاً من الرأس 0. قم أولاً بزيارة 0، ثم أي من جيرانه، على سبيل المثال 1. الآن تمت زيارة 1، كما هو موضح في الشكل أدناه (ب). لدى Vertex 1 ثلاثة جيران - 0، 2، و4. وبما أن 0 قد تمت زيارته بالفعل، فسوف تقوم بزيارة إما 2 أو 4. دعنا نختار 2. الآن تمت زيارة 2، كما هو موضح في الشكل أدناه (ج). لدى Vertex 2 ثلاثة جيران: 0 و1 و3. وبما أنه تمت زيارة 0 و1 بالفعل، اختر 3. تمت زيارة 3 الآن، كما هو موضح في الشكل أدناه (د). عند هذه النقطة، تمت زيارة القمم بهذا الترتيب:

0، 1، 2، 3

بما أن جميع جيران 3 قد تمت زيارتهم، قم بالتراجع إلى 2. بما أن جميع رؤوس 2 قد تمت زيارتها، فإن التراجع إلى 1. 4 مجاور لـ 1، ولكن لم تتم زيارة 4. لذلك قم بزيارة رقم 4 كما هو موضح في الشكل أدناه (هـ). بما أنه تمت زيارة جميع جيران الرقم 4، قم بالرجوع إلى الرقم 1.
بما أنه تمت زيارة جميع جيران الرقم 1، قم بالرجوع إلى 0. وبما أنه تمت زيارة جميع جيران الرقم 0، ينتهي البحث.

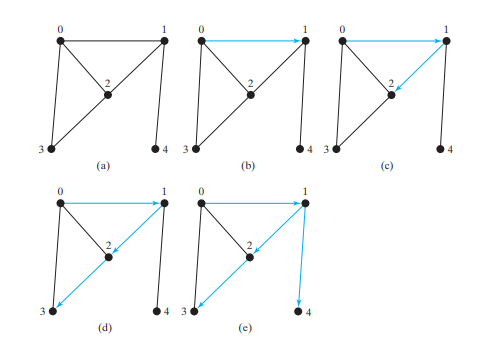
نظرًا لأنه تتم زيارة كل حافة وكل قمة مرة واحدة فقط، فإن التعقيد الزمني لطريقة dfs هو O(|E| |V|)، حيث |E | يشير إلى عدد الحواف و|V| يشير إلى عدد القمم.

تنفيذ بحث العمق أولاً

تستخدم خوارزمية DFS في الكود أعلاه العودية. ومن الطبيعي استخدام العودية لتنفيذه. وبدلاً من ذلك، يمكنك استخدام المكدس.

تم تطبيق الطريقة dfs(int v) في الأسطر 164-193 في AbstractGraph.java. تقوم بإرجاع مثيل للفئة Tree مع قمة الرأس v كجذر. تقوم الطريقة بتخزين القمم التي تم البحث عنها في القائمة searchOrder (السطر 165)، أصل كل قمة في المصفوفة parent (السطر 166)، وتستخدم isVisited مصفوفة للإشارة إلى ما إذا كان قد تمت زيارة قمة (السطر 171). يستدعي الأسلوب المساعد dfs(v,parent, searchOrder, isVisited) لإجراء بحث عميق أولاً (السطر 174).

في الطريقة المساعدة العودية، يبدأ البحث من قمة الرأس u. تتم إضافة u إلى searchOrder في السطر 184 ويتم وضع علامة "تمت زيارته" (السطر 185). لكل جار لم تتم زيارته لـ u، يتم استدعاء الطريقة بشكل متكرر لإجراء بحث عميق أولاً. عند زيارة قمة e.v، يتم تخزين أصل e.v في parent[e.v] (السطر 189). تُرجع الطريقة عند زيارة جميع القمم لرسم بياني متصل، أو في مكون متصل.

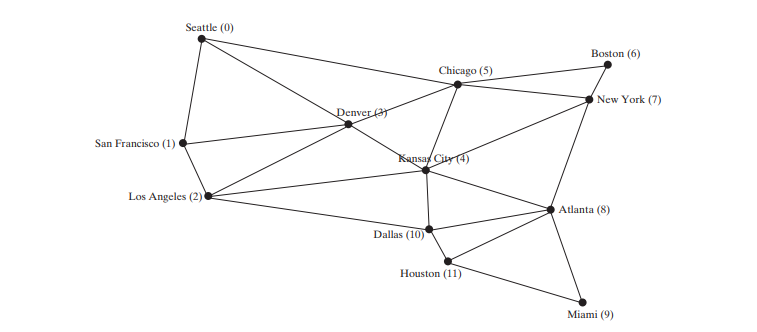
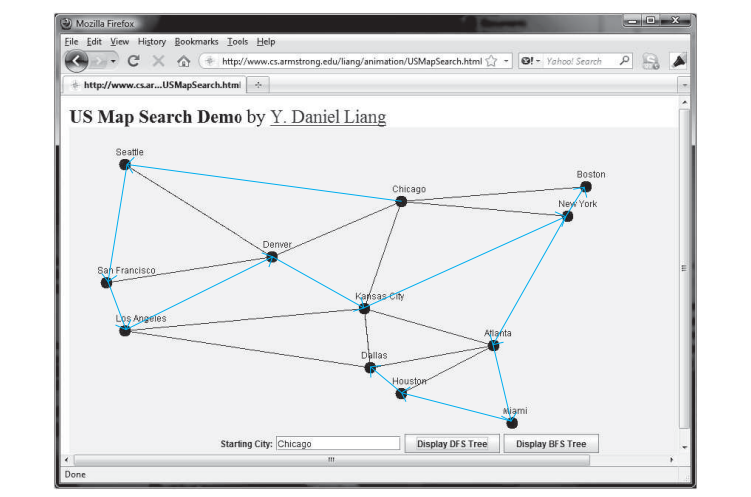
يوفر الكود أدناه برنامج اختبار يعرض DFS للرسم البياني في الشكل أعلاه بدءًا من شيكاغو. يظهر الرسم التوضيحي لـ DFS بدءًا من شيكاغو في الشكل أدناه.

public class TestDFS {

    public static void main(String[] args) {
        String[] vertices = {"Seattle", "San Francisco", "Los Angeles", "Denver", "Kansas City", "Chicago", "Boston", "New York", "Atlanta", "Miami", "Dallas", "Houston"};

        int[][] edges = {
                {0, 1}, {0, 3}, {0, 5},
                {1, 0}, {1, 2}, {1, 3},
                {2, 1}, {2, 3}, {2, 4}, {2, 10},
                {3, 0}, {3, 1}, {3, 2}, {3, 4}, {3, 5},
                {4, 2}, {4, 3}, {4, 5}, {4, 7}, {4, 8}, {4, 10},
                {5, 0}, {5, 3}, {5, 4}, {5, 6}, {5, 7},
                {6, 5}, {6, 7},
                {7, 4}, {7, 5}, {7, 6}, {7, 8},
                {8, 4}, {8, 7}, {8, 9}, {8, 10}, {8, 11},
                {9, 8}, {9, 11},
                {10, 2}, {10, 4}, {10, 8}, {10, 11},
                {11, 8}, {11, 9}, {11, 10}
        };

        Graph graph = new UnweightedGraph(vertices, edges);
        AbstractGraph.Tree dfs = graph.dfs(graph.getIndex("Chicago"));

        java.util.List searchOrders = dfs.getSearchOrder();
        System.out.println(dfs.getNumberOfVerticesFound()   " vertices are searched in this DFS order:");
        for(int i = 0; i 



يتم البحث عن 12 رأسًا بترتيب DFS هذا:

 شيكاغو سياتل سان فرانسيسكو لوس أنجلوس دنفر

 كانساس سيتي نيويورك بوسطن أتلانتا ميامي هيوستن دالاس

والدة سياتل هي شيكاغو

والد سان فرانسيسكو هو سياتل

والد لوس أنجلوس هو سان فرانسيسكو

والد دنفر هو لوس أنجلوس

والد مدينة كانساس سيتي هو دنفر

والد بوسطن هو نيويورك

والد نيويورك هو مدينة كانساس

والد أتلانتا هو نيويورك

والد ميامي هو أتلانتا

والدا دالاس هي هيوستن

والدة هيوستن هي ميامي




  
  
  تطبيقات DFS


يمكن استخدام بحث العمق أولاً لحل العديد من المشكلات، مثل ما يلي:

اكتشاف ما إذا كان الرسم البياني متصلاً. ابحث في الرسم البياني بدءًا من أي قمة. إذا كان عدد القمم التي تم البحث عنها هو نفس عدد القمم في الرسم البياني، فإن الرسم البياني متصل. وإلا فإن الرسم البياني غير متصل.
اكتشاف ما إذا كان هناك مسار بين قمتين.
إيجاد المسار بين قمتين.
العثور على جميع المكونات المتصلة. المكون المتصل هو رسم بياني فرعي متصل أقصى حيث يتم توصيل كل زوج من القمم بواسطة مسار.
اكتشاف ما إذا كانت هناك دورة في الرسم البياني.
إيجاد دورة في الرسم البياني.
العثور على مسار/دورة هاملتونية. مسار هاميلتون في الرسم البياني هو المسار الذي يزور كل قمة في الرسم البياني مرة واحدة بالضبط. تزور دورة هاميلتون كل قمة في الرسم البياني مرة واحدة بالضبط وتعود إلى قمة البداية.
يمكن حل المشكلات الستة الأولى بسهولة باستخدام طريقة dfs في AbstractGraph.java. للعثور على مسار/دورة هاميلتونية، عليك استكشاف جميع DFSs الممكنة للعثور على المسار الذي يؤدي إلى أطول مسار. للمسار/الدورة الهاملتونية العديد من التطبيقات، بما في ذلك حل مشكلة جولة الفارس المعروفة.